(取石子)Alice和Bob两个人在玩取石子游戏。他们制定了n条取石子的规则,第i条规则为:如果剩余石子的个数大于等于a[i]且大于等于b[il, 那么他们可以取走b[i]个石子。他们轮流取石子。如果轮到某个人取石子, 而他无法按照任何规则取走石子,那么他就输了。一开始石子有m个。请问先取石子的人是否有必胜的方法?
输入第一行有两个正整数,分别为规则个数n(1≤n≤64),以及石子个数m(≤10^7)。
接下来n行。第i行有两个正整数a[i]和b[i](1≤a[i]≤10^7,1≤b[i]≤64)
如果先取石子的人必胜,那么输出“Win”,否则输出“Loss”
提示:
可以使用动态规划解决这个问题。由于b[i]不超过64,所以可以使用64位无符号整数去压缩必要的状态。
status是胜负状态的二进制压缩,trans是状态转移的二进制压缩。
试补全程序。
代码说明:
“~”表示二进制补码运算符,它将每个二进制位的0变成1、1变为0;
而“^”表示二进制异或运算符,它将两个参与运算的数中的每个对应的二进制位一一进行比较,若两个二进制位相同,则运算结果的对应二进制位为0,反之为1。
ull标识符表示它前面的数字是unsigned long long 类型。
#include <cstdio>
#include<algorithm>
using namespace std ;
const int maxn =64;
int n,m;
int a[maxn],b[maxn];
unsigned long long status ,trans;
bool win;
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i<n; ++i)
scanf("%d%d", &a[i], &b[i]);
for(int i = 0; i < n; ++i)
for(int j = i + 1; j < n; ++j)
if (a[i] > a[j]) {
swap(a[i],a[j]);
swap(b[i],b[j]);
}
status = ___(1)___;
trans = 0;
for(int i = 1, j = 0; i <= m; ++i) {
while (j < n && ___(2)___) {
___(3)___
++j;
}
win = ___(4)___;
___(5)___;
}
puts(win ? "Win" : "Loss");
return 0;
}
①处应填()
0
~0u11
~0u11^1
1
②处应填()
a[j]<i
a[j]==i
a[j]!=i
a[j]>i
③处应填()

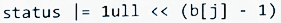
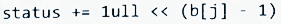

④处应填()
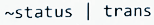
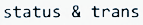
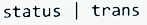

⑤处应填()



