组合题
（最优子序列）取m=6，给出长度为n的整数序列a1,a2，……an（0 ≤ ai<2m）。对于一个二进制数x,定义其分值w(x)为x + popcnt(x),其中 popcnt(x)表示x二进制表示中1的个数。对于一个子序列b1，b2，…，bk，定 义其子序列分值S为w（b1㊉b2）+w（b2㊉b3）+w（b3㊉b4）+……+w（bk-1㊉bk）。其中㊉表示按位异或。对于空子序列，规定其子序列分值为0。求一个子序列使得其子序列分值最大，输出这个最大值。
输入第一行包含一个整数n(1 ≤ n ≤ 40000).接下来一行包含n个整数 a1，a2，……，an。
提示：考虑优化朴素的动态规划算法，将前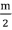
位和后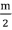位分开计算。
Max[x][y]表示当前的子序列下一个位置的高8位是X、最后一个位置的 低8位是y时的最大价值。
试补全程序。
第1题
单选题
①处应填（）
A
X >>= 1
B
X ^=X & (x ^ (x + 1))
C
X -= X | -X
D
X ^= X & (X ^ (x - 1))
第2题
单选题
②处应填（）
A
(a & MS) « B
B
a>>B
C
a&(1<<B)
D
a&(MS<<B)
第3题
单选题
③处应填（）
A
-INF
B
Max[y] [x]
C
0
D
Max[x][yJ
第4题
单选题
④处应填（）
A
Max[x] [z]+w（y^z）
B
Max[x][z] + w(a ^ z)
C
Max[x] [z]+w（x^(z<<B）)
D
Max[x][z] + w(x ^ z)
第5题
单选题
⑤处应填()
A
to_max(Max[y][z],v + w(a ^(z << B)))
B
to_max(Max[z][y],v + w((x ^ z) << B))
C
to_max(Max[zJ[y],v + w(a ^ (z << B)))
D
to_max(Max[x][z],v + w(y ^ z))