(最大值之和)给定整数序列a0,… an-1,求该序列所有非空连续子序列的最大值之和。上述参数满足1≤n≤105和1≤a;≤108。
一个序列的非空连续子序列可以用两个下标l和r(其中0≤l≤r<n)表示,对应的序列为alal+1… ar。两个非空连续子序列不同,当且仅当下标不同。
例如,当原序列为[1,2,1,2]时,要计算子序列[1]、[2]、[1]、[2]、[1,2]、[2,1]、[1,2]、[1,2,1]、[2,1,2]、[1,2,1,2]的最大值之和,答案为18。注意[1,1]和[22]虽然是原序列的子序列,但不是连续子序列,所以不应该被计算。另外,注意其中有一些值相同的子序列,但由于他们在原序列中的下标不同,属于不同的非空连续子序列,所以会被分别计算。解决该问题有许多算法,以下程序使用分治算法,时间复杂度0(nlogn)。
试补全程序。
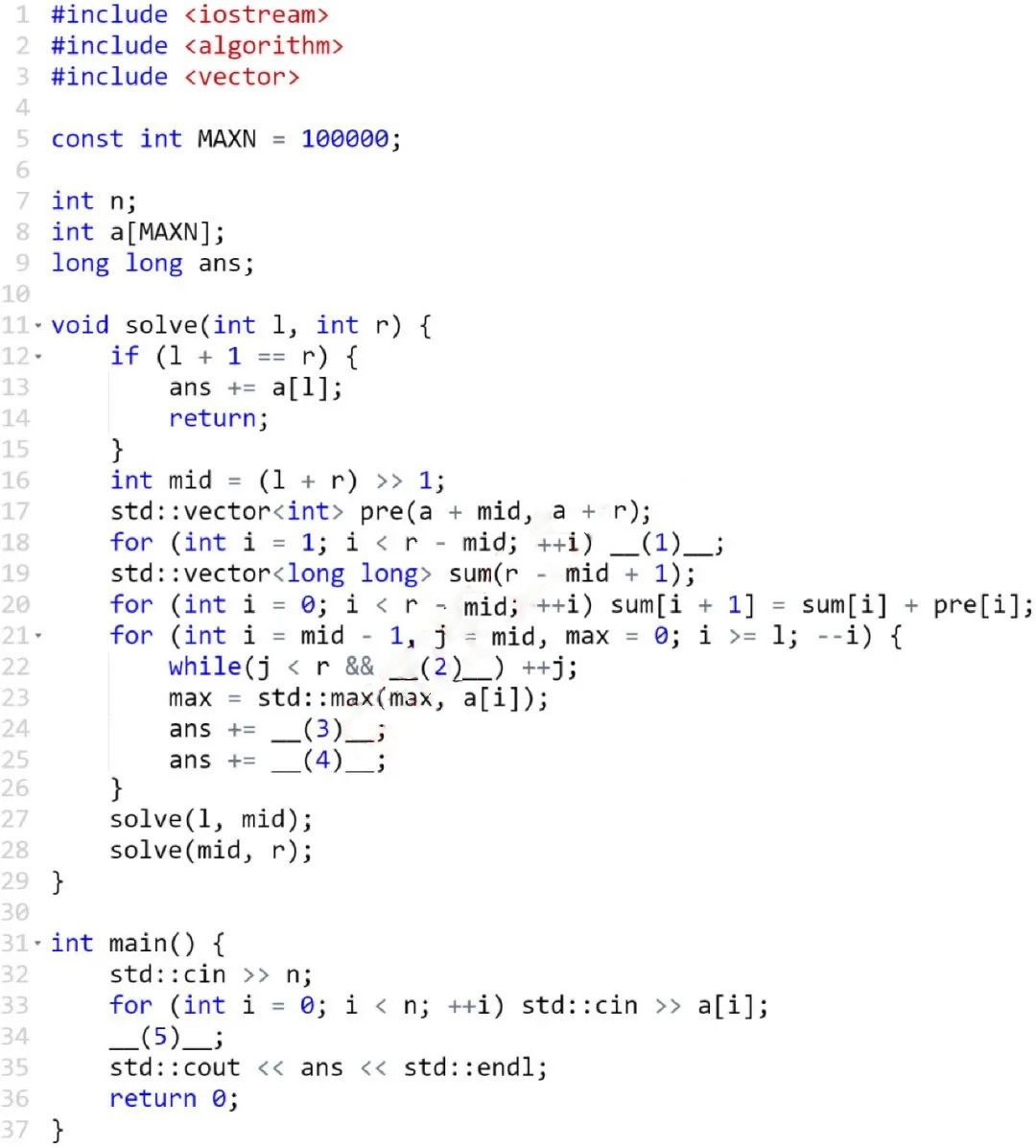
①处应填()
pre[i]= std::max(pre[i- 1],a[i-1])
pre[i+1]= std:max(pre[i],pre[i+1])
pre[i]= std;:max(pre[i-1],a[i])
pre[i]= std:max(pre[i], pre[i- 1])
②处应填()
a[j]< max
a[j]<a[i]
pre[j-mid]<max
pre[j- mid]> max
③处应填()
(long long)(j -mid)* max
(long long)(j- mid)*(i-1)*max
sum[j- mid]
sum[j-mid]*(i-1)
④处应填()
(long long)(r-j)*max
(long long)(r-j)*(mid -i)*max
sum[r- mid]- sum[-mid]
(sum[r-mid]- sum[j-mid])*(mid-i)
⑤处应填()
solve(0,n)
solve(0, n-1)
solve(1,n)
solve(1, n-1)