希尔伯特曲线

题目描述

希尔伯特曲线是以下一系列分形曲线 Hn 的极限。我们可以把 Hn 看作一条覆盖 2^n × 2^n 方格矩阵的曲线，曲线上一共有 2^n × 2^n 个顶点(包括左下角起点和右下角终点)，恰好覆盖每个方格一次。

Hn(n > 1)可以通过如下方法构造：

1. 将 Hn-1 顺时针旋转90度放在左下角

2. 将 Hn-1 逆时针旋转90度放在右下角

3. 将2个 Hn-1 分别放在左上角和右上角

4. 用3条单位线段把4部分连接起来

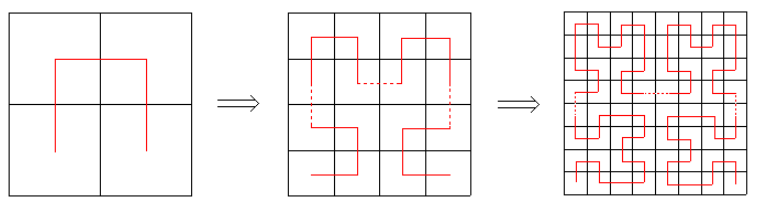
对于 Hn 上每一个顶点 p ，我们定义 p 的坐标是它覆盖的小方格在矩阵中的坐标(左下角是(1, 1)，右上角是(2^n, 2^n)，从左到右是X轴正方向，从下到上是Y轴正方向)，

定义 p 的序号是它在曲线上从起点开始数第几个顶点(从1开始计数)。

以下程序对于给定的n(n <= 30)和p点坐标(x, y)，输出p点的序号。请仔细阅读分析源码，填写划线部分缺失的内容。

#include <stdio.h>

long long f(int n, int x, int y) {

    if (n == 0) return 1;

    int m = 1 << (n - 1);

    if (x <= m && y <= m) {

        return f(n - 1, y, x);

    }

    if (x > m && y <= m) {

        return 3LL * m * m + f(n - 1, ________________ , m * 2 - x + 1); //  填空

    }

    if (x <= m && y > m) {

        return 1LL * m * m + f(n - 1, x, y - m);

    }

    if (x > m && y > m) {

        return 2LL * m * m + f(n - 1, x - m, y - m);

    }

}

int main() {

 int n, x, y;

    scanf("%d %d %d", &n, &x, &y); 

    printf("%lld", f(n, x, y));

    return 0;

}

注意：只填写划线处缺少的内容，不要填写已有的代码或符号，也不要填写任何解释说明文字等。