### 问题描述 魏国突发大水，百姓困苦不堪，曹操派遣谋士郭嘉与司马懿前往各地救灾。 具体来说，魏国共有 $N$ 座城市，之间由 $N-1$ 条道路相连，其中第 $i$ 条道路连接城市 $u_i$ 和 $v_i$。确保任何一座城市都可以通过现有的道路到达其他城市。 郭嘉和司马懿需要在 $M$ 天内完成救灾工作。两人最初都位于 $1$ 号城市。在第 $i(1 \leq i \leq M)$ 天，城市 $A_i$ 和 $B_i$ 需要救援，两人需商议各自前往的城市，并有以下约定： - 若 $i$ 为奇数，则郭嘉可以优先选择前往城市 $A_i$ 或 $B_i$，如果郭嘉选择前往 $A_i$，则司马懿就只能前往 $B_i$；如果郭嘉选择前往 $B_i$，则司马懿就只能前往 $A_i$。 - 若 $i$ 为偶数，则司马懿可以优先选择前往城市 $A_i$ 或 $B_i$，如果司马懿选择前往 $A_i$，则郭嘉就只能前往 $B_i$；如果司马懿选择前往 $B_i$，则郭嘉就只能前往 $A_i$。 两人都希望最大化自己的行动距离，以彰显他们的辛劳，从而赢得曹操的赞赏。 即设郭嘉走的总距离为 $x$，司马懿走的总距离为 $y$。郭嘉希望最大化 $x-y$ 的值，而司马懿则希望最小化 $x-y$ 的值。假设两人都按照最优策略行事，问 $x-y$ 的值是多少？ **注意：两人在完成每次救灾任务后会停留在当前城市过夜，且可能存在某一天 $A_i = B_i$ 的情况。** ### 输入格式 第一行输入两个整数 $N,M(1 \leq N,M \leq 10^5)$ 表示城市的数量和救灾工作天数。 接下来 $N-1$ 行每行输入两个整数 $u,v (1 \leq u,v \leq N, u \ne v)$ 表示城市 $u,v$ 之间存在一条道路。 接下来 $M$ 行，每行两个整数 $A_i,B_i(1 \leq A_i,B_i \leq N)$ 表示第 $i$ 天需要被救灾的城市。 ### 输出格式 输出一个整数表示答案。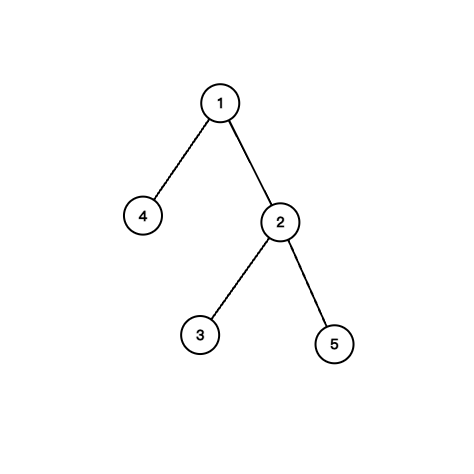 ### 输入样例 ```text 5 2 1 2 2 3 1 4 5 2 5 4 2 3 ``` ### 输出样例 ```text -1 ``` ### 样例说明 对于样例，无论郭嘉第一天选择几号城市，只要司马懿第二天选择 $3$ 号城市，$x-y$ 的值就都会为 $-1$。