编程题
### 问题描述
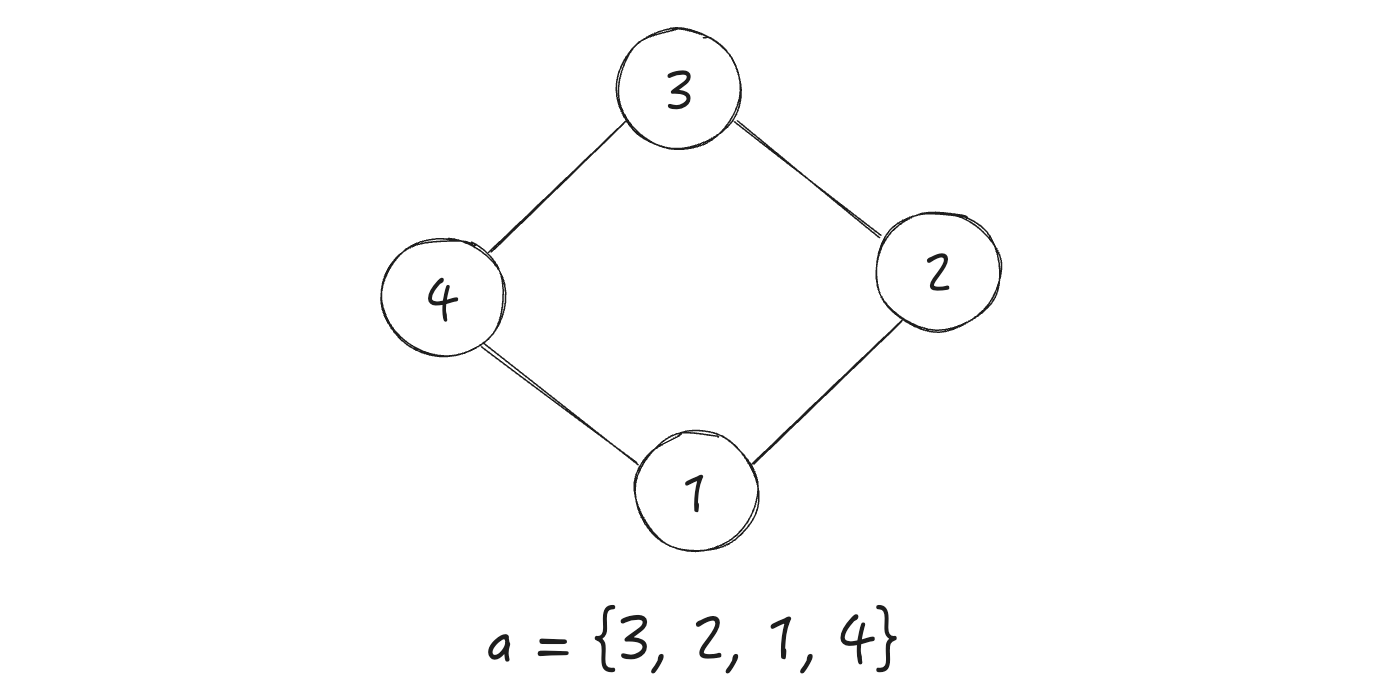
在六一儿童节的庆祝活动中,蓝桥学院组织了一个游戏。游戏邀请了 $n$ 个孩子参与,每个孩子被赋予了一个独一无二的编号,从 $1$ 到 $n$。
游戏开始前,孩子们将按照给定的编号序列 $\{a_1, a_2, \dots, a_n\}$ 手拉手排成一个圈。编号为 $a_1$ 的孩子与编号为 $a_2$、$a_n$ 的孩子手拉手,编号为 $a_2$ 的孩子与编号为 $a_1$、$a_3$ 的孩子手拉手,以此类推。
 游戏过程中,老师会进行 $q$ 次操作。每次操作,老师会选择两个不同编号的孩子,并交换他们的位置。
在每次交换后,孩子们需要从圈中选出两个**相邻**的孩子松开手,形成一个队列。**这个队列可以从任意方向观察**,如果队列的编号是有序的(单调递增或单调递减),那么孩子们将获得礼物;反之,孩子们将无法获得礼物。
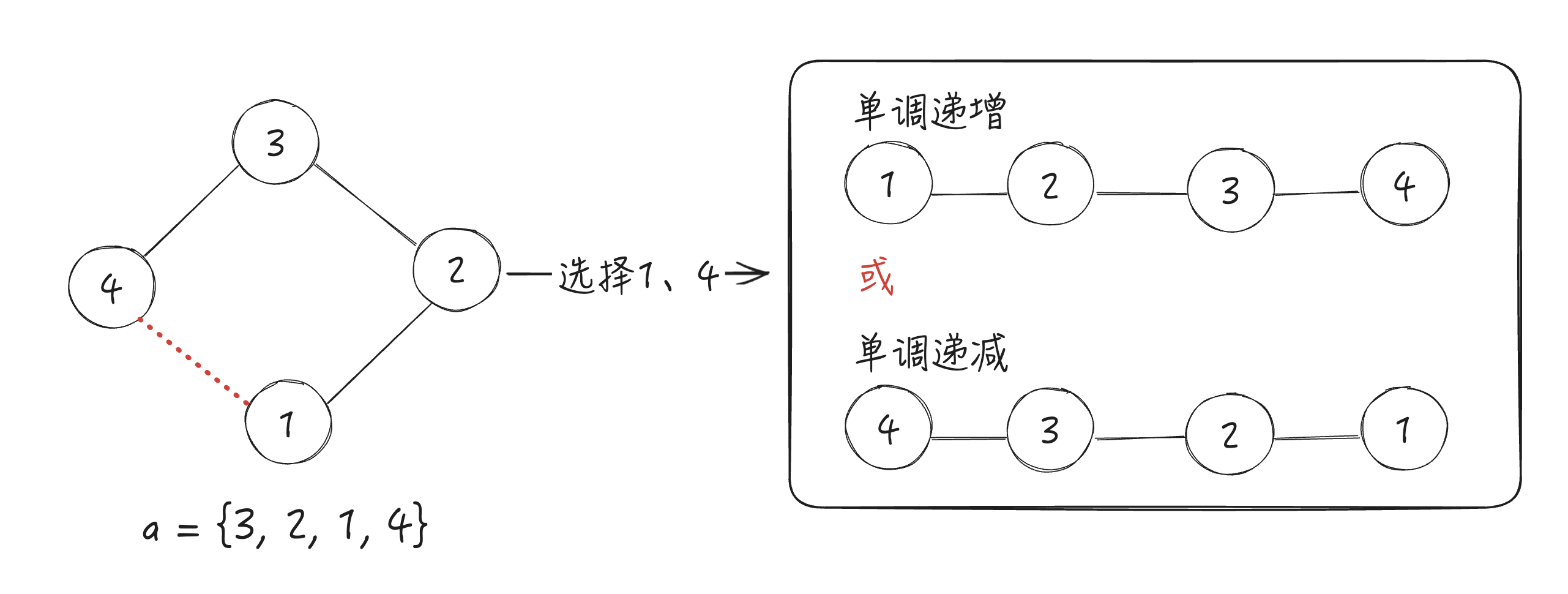
现在,请你帮助孩子们判断,在每次交换后,是否存在一种方式,能够通过让一对相邻孩子松手,使得剩下的孩子排成一个有序的队列。
### 输入格式
输入的第一行包含两个整数 $n$ 和 $q$($3\leq n\leq 10^5,1\leq q\leq 10^5$),表示孩子的数量和操作的次数。
接下来一行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$($1\leq a_i \leq n$,$a_1,a_2,\dots, a_n$ 各不相同),表示初始时孩子们的编号序列。
接下来 $q$ 行,每行包含两个整数 $x$ 和 $y$($1\leq x,y \leq n$,$x\neq y$),表示一次操作中需要交换位置的两个孩子的编号。
### 输出格式
输出共 $q$ 行,每行输出一个字符串,表示每次操作后是否存在一种方式使得剩下的孩子排成一个有序的队列。如果存在,输出 `Yes`,否则输出 `No`。
### 样例输出
```text
5 3
1 2 3 4 5
2 4
1 5
1 3
```
### 样例输出
```
No
Yes
No
```
### 样例说明
在第一次操作后,孩子们的编号序列为 $\lbrace 1, 4, 3, 2, 5\rbrace $,无法通过让一对相邻孩子松手使得剩下的孩子排成有序队列。
在第二次操作后,孩子们的编号序列为 $\lbrace 5, 4, 3, 2, 1\rbrace $,可以通过让编号为 $1$ 和 $5$ 的孩子松手,使得剩下的孩子排成有序的队列:
$$
1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 5
$$
在第三次操作后,孩子们的编号序列为 $\lbrace 5, 4, 1, 2, 3\rbrace$,无法通过让一对相邻孩子松手使得剩下的孩子排成有序队列。
游戏过程中,老师会进行 $q$ 次操作。每次操作,老师会选择两个不同编号的孩子,并交换他们的位置。
在每次交换后,孩子们需要从圈中选出两个**相邻**的孩子松开手,形成一个队列。**这个队列可以从任意方向观察**,如果队列的编号是有序的(单调递增或单调递减),那么孩子们将获得礼物;反之,孩子们将无法获得礼物。

现在,请你帮助孩子们判断,在每次交换后,是否存在一种方式,能够通过让一对相邻孩子松手,使得剩下的孩子排成一个有序的队列。
### 输入格式
输入的第一行包含两个整数 $n$ 和 $q$($3\leq n\leq 10^5,1\leq q\leq 10^5$),表示孩子的数量和操作的次数。
接下来一行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$($1\leq a_i \leq n$,$a_1,a_2,\dots, a_n$ 各不相同),表示初始时孩子们的编号序列。
接下来 $q$ 行,每行包含两个整数 $x$ 和 $y$($1\leq x,y \leq n$,$x\neq y$),表示一次操作中需要交换位置的两个孩子的编号。
### 输出格式
输出共 $q$ 行,每行输出一个字符串,表示每次操作后是否存在一种方式使得剩下的孩子排成一个有序的队列。如果存在,输出 `Yes`,否则输出 `No`。
### 样例输出
```text
5 3
1 2 3 4 5
2 4
1 5
1 3
```
### 样例输出
```
No
Yes
No
```
### 样例说明
在第一次操作后,孩子们的编号序列为 $\lbrace 1, 4, 3, 2, 5\rbrace $,无法通过让一对相邻孩子松手使得剩下的孩子排成有序队列。
在第二次操作后,孩子们的编号序列为 $\lbrace 5, 4, 3, 2, 1\rbrace $,可以通过让编号为 $1$ 和 $5$ 的孩子松手,使得剩下的孩子排成有序的队列:
$$
1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 5
$$
在第三次操作后,孩子们的编号序列为 $\lbrace 5, 4, 1, 2, 3\rbrace$,无法通过让一对相邻孩子松手使得剩下的孩子排成有序队列。