编程题
### 问题描述
小蓝对医学研究充满了热情,他一直致力于寻找一种能够改善人类健康的特殊药物。他深知,药物的分子结构对其治疗效果至关重要,因此他决定展开一项关于药物分子排列的实验。
实验的第一步,小蓝准备了 $n$ 个不同类型的分子,编号从 $1$ 到 $n$。然后,他设计了一个包含 $k$ 个位置的直线型模拟基座,用于放置这些分子。
实验的规则简单而明确:首先,小蓝会将编号为 $1$ 的分子放置在模拟基座的任意一个位置。接着,他会按照编号 $2$ 到 $n$ 的顺序,将每个分子**依次**放置在与上一个分子的相邻的任意位置。如果该位置已被占据,则将新分子放置在已有分子的上层。
实验完成后,小蓝会记录模拟基座上每个位置最顶层的分子编号,如果某位置没有分子,则记为 $0$。显然,不同的放置方式可能会导致不同的顶层分子序列。
对此,小蓝想知道,在所有可能的分子放置方式中,有多少种不同的顶层分子序列可能出现。两个序列被视为不同,如果它们在至少一个位置上的分子编号不同。
请你帮助小蓝计算出不同顶层分子序列的总数,并将结果对 $998244353$ 取模。
### 输入格式
输入仅一行,包含两个整数 $n$ 和 $k$($1\leq n ,k \leq 2\times 10^3$),分别表示分子的数量和模拟基座的位置数。
### 输出格式
输出一个整数,表示不同的顶层分子序列的数量,结果对 $998244353$ 取模。
### 样例输入
```text
3 3
```
### 样例输出
```text
6
```
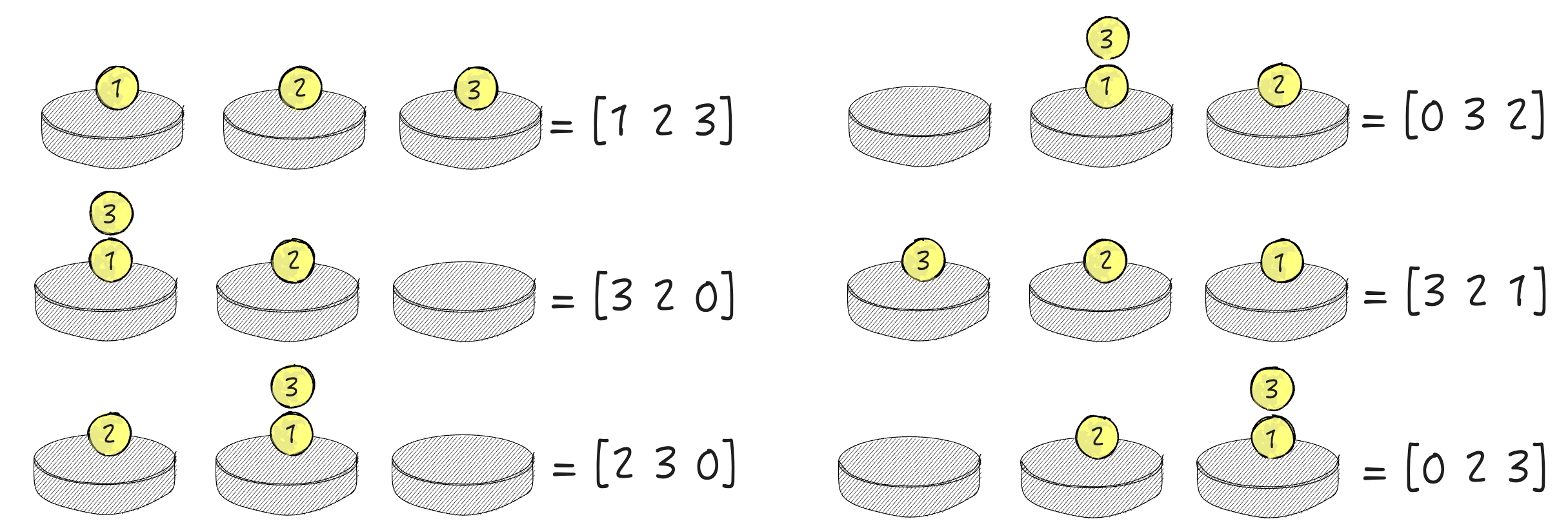
### 样例说明