### 问题描述 小桥是一名外卖小哥，他收到很多的订单需要送。 他所在城市的地图可以看成一幅无向连通图，其中有 $n$ 个节点，编号为 $1 \sim n$，有 $m$ 条边。 每一笔订单由两个参数 $(s_i,t_i)$ 组成，表示他需要从 $s_i$ 点出发，将外卖送到 $t_i$ 点。小桥可以随意规定他的路线，但是为了追求效率，**在每一笔订单中，每条边只能经过一遍。** 同时小桥是一个相信幸运的人，城市的某些路上装配了一些刮刮乐彩票机，小桥想知道在他的每笔订单中，是否有机会买彩票。 **注意，每笔订单是独立的，每笔订单的过程只计算从 $s_i$ 出发到 $t_i$ 结束，你无须关注从 $t_i$ 到 $s_{i+1}$ 的过程。** ### 输入格式 第一行输出一个整数 $T$，表示有 $T$ 组数据。 每组数据由以下部分组成： 第一行输入三个整数 $n,m,q$，$n$ 代表城市节点的数量，$m$ 代表边的数量，$q$ 代表订单的数量。 接下来 $m$ 行描述道路，三个整数 $v_i, u_i, f_i$，表示存在一条 $(v_i, u_i)$ 的道路，$f_i$ 为 $1$ 时表示这条路上装配了刮刮乐彩票机，$f_i$ 为 $0$ 时表示这条路上未装配彩票机。 接下来 $q$ 行描述订单，两个整数 $(s_i, t_i)$ ，表示他需要从 $s_i$ 点出发，将外卖送到 $t_i$ 点。（由于是连通图，所有一定能到达）。 数据规模约定： $1 \le n,q\le10^5, 0 \le m \le 2 \times10^5, \sum n \le 10^6,\sum m \le 2 \times 10^6,\sum q \le 10^6, f_i \in \lbrace 0,1\rbrace, 1\le T \le 10^6$。 $v_i,u_i,s_i,t_i \in [1, n]$。 图中可以存在重边，自环。 ### 输出格式 对于每个询问，输出一个字符串： 如果可以买彩票，输出：`Yes`。 如果不可以，输出：`No`。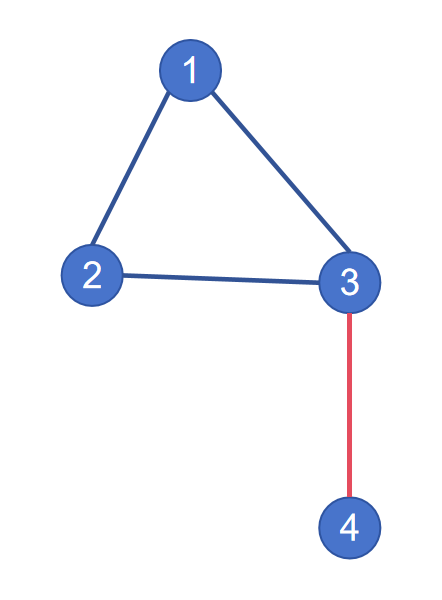 ### 样例输入 ```bash 1 4 4 2 1 2 0 1 3 0 2 3 0 3 4 1 1 4 1 3 ``` ### 样例输出 ```bash Yes No ``` ### 说明 $1 \to 4$ 能够经过带有彩票的道路（红色边）。 $1 \to 3$ 不能够经过带有彩票的道路。