### 问题描述 小蓝面对一个 $n \times m$ 的矩形 $D$，其中每个位置 $(i, j)$ 上都有一个元素 $x_{i,j}$。 我们定义两个函数 $f(D)$、$g(D)$，$f(D)$ 的值为矩阵 $D$ 的所有元素的和值，$g(D)$ 为矩阵 $D$ 的极差，即矩阵中的最大值减去最小值。 他需要在这个矩形中选择一个 $n' \times m' $ 的**连续子矩阵**，记为矩阵 $D'$，他希望选择的连续子矩阵 $D'$ 能够使得 $f(D') \times g(D')$ 最大化。 小蓝知道你很聪明，于是他把问题交给了你，希望你回答他最大化的值是多少。 连续子矩阵：是在原矩阵选取部分**连续行**、**连续列**所组成的新矩阵。 ### 输入格式 第一行包含四个整数 $n,m,n',m'$（$n\times m \le 10^6, 1 \le n' \le n, 1 \le m' \le m$），表示矩形的行数和列数，以及你需要选择的子矩阵的行数和列数。 接下来 $n$ 行，每行包含 $m$ 个整数，表示矩形中每个位置的元素值 $x_{i,j}$（$1 \le x_{i,j} \le 10^6$）。 输入量较大，建议采用较快的输入输出方式。 ### 输出格式 一个整数，代表最大化的值。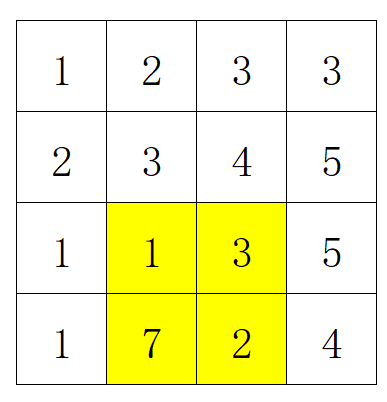 ### 样例输入 ```bash 4 4 2 2 1 2 3 3 2 3 4 5 1 1 3 5 1 7 2 4 ``` ### 样例输出 ```bash 78 ``` ### 说明 选择的连续子矩阵如下图黄色部分所示： $f(D')=13, g(D')=6$。