### 问题描述 现有 $2N$ 个红色木棍和 $N$ 个蓝色木棍。 红色木棍的集合由一个长度为 $N$ 的正整数序列 $A$ 表示，序列中每存在一个 $A_i$ 表示有 $2$ 个长度为 $A_i$ 的红色木棍； 蓝色木棍的集合由一个长度为 $N$ 的正整数序列 $B$ 表示，序列中每存在一个 $B_i$ 表示有 $1$ 个长度为 $B_i$ 的蓝色木棍。 现在要求用 $3$ 个木棍组成一个等腰三角形，每个三角形中要包含 $2$ 个红色木棍以及 $1$ 个蓝色木棍，并且要求 $2$ 个红色木棍的长度相等。 求最多可以组成多少个这样的三角形。 ### 输入格式 第一行输入 $1$ 个正整数 $N$（$1 \leq N \leq 200000$），表示序列 $A, B$ 的长度。 第二行输入 $N$ 个正整数 $A_1, A_2, \dots, A_N$（$1\leq A_i\leq 10^9$），表示序列 $A$。 第三行输入 $N$ 个正整数 $B_1,B_2,\dots, B_N$（$1\leq B_i \leq 10^9$），表示序列 $B$。 ### 输出格式 输出仅一行，包含 $1$ 个整数，表示答案。 ### 样例输入 ```text 4 4 3 2 1 2 4 3 2 ``` ### 样例输出 ```text 3 ``` ### 样例说明 两个长度为 $1$ 的红色木棍无法与给出的蓝色木棍组成三角形。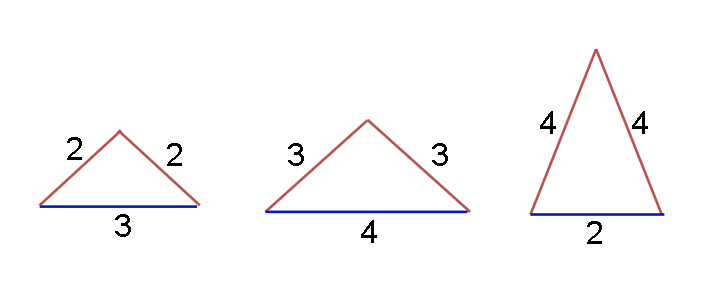 $ ({\color{red}2}, {\color{red}2}, {\color{blue}3}), ({\color{red}3}, {\color{red}3}, {\color{blue}4}), ({\color{red}4}, {\color{red}4}, {\color{blue}2})$ 是一组解。