### 问题描述 小桥被小蓝的数学题考验之后，变得十分愤怒。于是他想要抓住小蓝，并狂暴输出一万个数学题来考验小蓝。 他们所在的世界可以看成是由 $n$ 个节点，$n-1$ 条边组成的一副树形图，小桥在 $1$ 号点，小蓝会等概率的出现在 $1 \sim n$ 中的某一个点。 每一秒，两人都能移动到他们当前位置相邻的节点，或者也可以选择不移动。当小蓝和小桥处于同一个位置时，可以认为小桥抓住了小蓝。 **注意**：两人的移动是线性的，他们会沿着边等速移动，所以他们也可能在路中间相遇。 小蓝，小桥都是很聪明的，无论出现在哪一个点，小蓝总会逃跑尽可能长的时间，以坚持最长的时间不被小桥抓住，而小桥也会尽可能以最短的时间抓出小蓝。 现在，请你计算一下小蓝能坚持的最长时间的**期望**是多少？答案可能不是整数，请对 $998244353$ 取模。 ### 输入格式 第一行输入一个整数 $n$。（$2 \le n \le 10^6$）。 接下来 $n - 1$ 行，每行输入 $2$ 个整数 $u_i, v_i$，表示存在一条边连接 $(u_i, v_i)$。（$ 1 \le u_i, v_i \le n$）。 保证数据是一棵树。 ### 输出格式 输出一个整数，表示期望能坚持的最长时间。答案对 $998244353$ 取模。 如果答案是 $\frac {a}{b}$ 的形式，你需要输出 $a \times b^{-1} \mod 998244353$，$b^{-1}$ 是 $b$ 在模 $998244353$ 下的逆元，题目保证答案一定存在。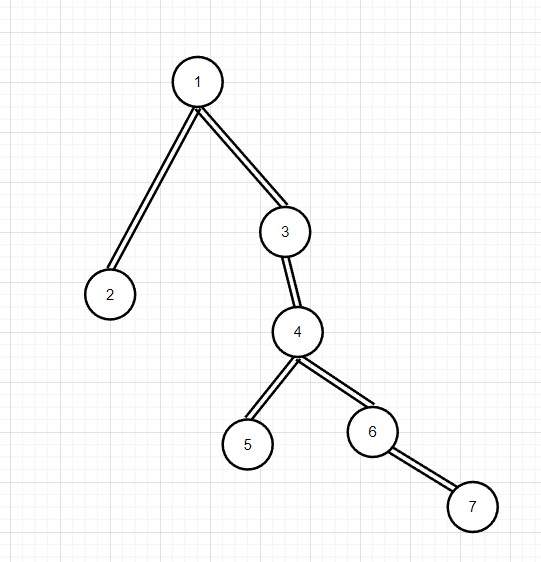 ### 样例输入 ```bash 7 1 2 1 3 3 4 5 4 6 4 6 7 ``` ### 样例输出 ```bash 3 ``` ### 说明  1. 出现在 $1$ 点，最晚 $0$ 秒时被抓住。 2. 出现在 $2$ 点，最晚 $1$ 秒时被抓住。 3. 出现在 $3$ 点，最晚 $4$ 秒时被抓住。 4. 出现在 $4$ 点，最晚 $4$ 秒时被抓住。 5. 出现在 $5$ 点，最晚 $4$ 秒时被抓住。 6. 出现在 $6$ 点，最晚 $4$ 秒时被抓住。 7. 出现在 $7$ 点，最晚 $4$ 秒时被抓住。 所以期望是 $3$ 秒被抓住。