### 问题描述 小蓝家的房顶是一个边长为 $n$ 的正方形，可以看成是由 $n \times n$ 个边长为 $1$ 的小正方形格子组成。 从上到下第 $i$ 行、从左到右第 $j$ 列的格子用 $(i,j)$ 表示。 小蓝的家由于年久失修，导致房顶有一些地方漏水。总共有 $m$ 处漏水的地方，我们用 $(x_1, y_1),(x_2,y_2)...(x_m,y_m)$ 来表示。 于是小蓝来到了五金店，五金店贩卖着一些**正方形木板**，木板的种类有 $n$ 种，第 $i$ 种木板的边长为 $i$。小蓝需要**一块**能够覆盖**所有漏洞**的木板，请问小蓝需要购买木板的最小边长是多少？ ### 输入格式 第一行输入两个整数 $n,m$。 接下面 $m$ 行，每行两个整数 $(x_i, y_i)$ 代表第 $i$ 个漏洞的位置。 ### 输出格式 输出一个整数，代表木板的最小边长。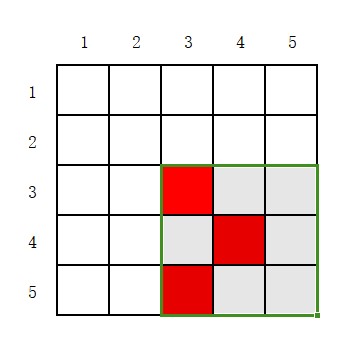 ### 样例输入 ```bash 5 3 3 3 5 3 4 4 ``` ### 样例输出 ``` 3 ``` ### 说明 房顶漏洞如下图所示，使用 $3 \times 3$ 的正方形可以覆盖掉所有的漏洞。  ### 评测数据范围 $2 \le n \le 10^{10}, 1 \le m \le \min(n^2, 10^4), 1 \le x_i,y_i \le n$。 保证所有的 $(x_i, y_i)$ 互不相同。