### 问题描述 城市建设离不开方便便捷的公共交通。X 市市政部门拟新建 $n$ 座公共汽车车站，并且初步制定了 $m$ 条线路。这些车站中有一个始发站和一个终点站，不管途径哪些车站公共汽车都必须从始发车站出发到达终点车站。 为了节约成本，实际设计路线的时候要去除一些冗余路线。也就是说只要保证所有站点都能从始发车站出发到达，所有车站都能到达终点车站就可以了，其余线路都是冗余的。为了最大程度地节约成本，你需要确定最多能去除多少条路线以后还能保证线路图是完整的（也就是满足前面提到的条件）。 ### 输入描述 第一行输入两个整数 $n,m$ ， $n$ 是公共汽车站的数量（其中包含了始发站和终点站）， $m$ 是市政部门初步指定的路线数量。 接下来输入 $m$ 行，每行包含两个整数 $x,y$ ，表示有一条 $x$ 到 $y$ 的路径（所有路径都是有方向的）。 站点用 $1$ 到 $n$ 之间的整数编号，同时保证所有路线连接唯一的站点对，没有路线连接到自身。在输入中，有一个站点没有接收到公共汽车，它是始发站。同样，从一个站点没有公共汽车行驶到任何其他站点，它是终点站。 数据保证： $1 \leq n \leq 2000，0 \leq m \leq 5000$ 。 ### 输出描述 输出一个整数，指可以从公共汽车网络系统中移除的路线的最大数量。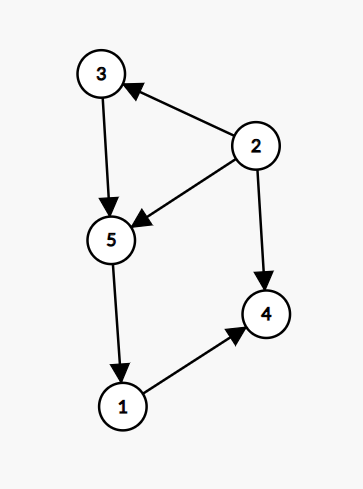 ### 样例输入 ``` 5 6 2 4 3 5 2 5 1 4 2 3 5 1 ``` ### 样例输出 ``` 2 ``` ### 说明 输入样例中描述的图：  图中 $2$ 车站没有接收到公共汽车， $4$ 车站没有公共汽车行驶到任何其他站点，他们分别是出发车站和终点车站。我们可以去掉 $2$ 到 $4$ 和 $2$ 到 $5$ 两条路，这样仍能保证所有站点都可以从出发车站到达，并最终到达终点车站。