编程题
### 问题描述
楼房的稳定程度通常取决于其地基的质量。然而,并非所有土地都适合作为地基。我们可以简单地描述这个问题:给定 $n$ 个适合作为地基的点,从中选择 $4$ 个点,使它们能够围成一个边平行于坐标轴的正方形。我们将正方形的边长定义为楼房的稳定程度。为了使楼房尽可能稳定,请计算可构建的最大正方形的边长。
### 输入描述
输入中包含多组测试数据。
每一组测试数据:
首先输入一个数字 $n$ ,表示适合作为地基的点的数量。
接下来输入 $n$ 行,每行输入两个整数 $x_i,y_i$ ,表示第 $i$ 个适合作为地基的点的坐标。
数据保证: $1 \leq n \leq 10^5,-10^9 \leq x_i,y_i \leq 10^9$ 。
### 输出描述
输出一个数字表示可构建的最大正方形的边长。
### 样例输入
```
3
0 0
0 1
1 0
8
0 10
0 20
0 30
10 0
10 10
10 20
20 0
20 10
```
### 样例输出
```
0
10
```
### 说明
对于第一组测试数据来说显然不能构成正方形,所以输出 $0$ 。
对于第二组测试数据,把所有点画在坐标系中:
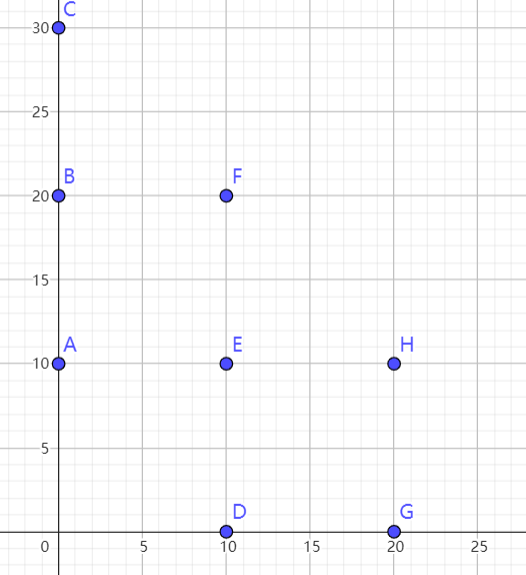
可以发现最大的正方形就是 $ABEF$ 或 $DEHG$ ,边长均为 $10$ 。