### 问题描述 聪明的 P 哥哥送给笨怂一个魔塔，让笨怂开始他的游戏。 以下是 P 哥哥对笨怂介绍魔塔的方式： - 魔塔的形状类似于一棵"树"，即魔塔中有多个节点，每个节点都可以连接到若干个子节点，并且魔塔中不存在环路。 - 每两个节点之间都有一条通道，可以通过通道从一个节点到达另一个节点。 - 每条通道都有两种状态：开和关。切换通道状态的开关位于当前通道所连接的父节点上。 - 每个开关控制多条通道，但在同一时刻只有一条通道的状态可以是开的。 - 每次触碰开关，该开关控制的通道中的开通道将关闭，而下一条通道将打开。如果关闭了最后一条通道，将打开第一条通道。 笨怂会从根节点开始，依次扔 $m$ 个小球，每个小球掉落到对应的节点时一定会触碰到开关。请你预测这 $m$ 个小球分别会停在哪个节点上。 ### 输入描述 第一行包含 $n,m$ ，表示魔塔中有 $n$ 个结点，笨怂向魔塔中扔 $m$ 个小球。 接下来输入 $n$ 个整数，第 $i$ 个数字 $w_i$ 表示 $i$ 结点的父结点为 $w_i$ 。 $i$ 从 $1$ 开始计数，结点的编号为 $0$ 到 $n-1$ ，其中根节点编号为 $0$ 。若输入多个结点的父结点相同，则输入的先后顺序即道路的顺序，也就是道路状态变为开的顺序。 数据保证： $1 \leq n,m \leq 3 \times 10^5$ 。 ### 输出描述 输出 $m$ 行，第 $i$ 行输出第 $i$ 个小球最终会停留在的结点的编号。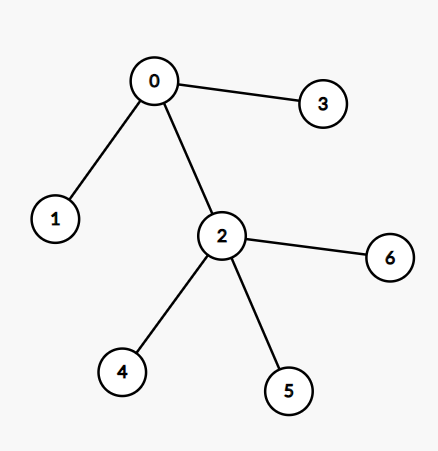 ### 样例输入 ``` 7 10 0 0 0 2 2 2 ``` ### 样例输出 ``` 1 4 3 1 5 3 1 6 3 1 ``` ### 说明 样例输入中描述的树：  | 打开的开关 | 最终会停留在的结点 | | ---------------------------- | --------- | | 0-1 2-4 | 1 | | 0-2 2-4（上一次未触碰到位于 $2$ 结点的开关） | 4 | | 0-3 2-5 | 3 | | 0-1 2-5 | 1 | | 0-2 2-5 | 5 | | 0-3 2-6 | 3 | | 0-1 2-6 | 1 | | 0-2 2-6 | 6 | | 0-3 2-4 | 3 | | 0-1 2-4 | 1 |