### 问题描述

在一个古老的城市遗迹中，探险家执梗正在尝试解开一个谜题。这个谜题包含一个复杂的网络，由 $n$ 个节点和 $m$ 条通道组成，其中第 $i$ 条通道的长度等于 $2^i$ 。执梗的任务是找到一个最短的闭环。

闭环是原网络的一个子网络，包含 $k$ （ $3 \leq k \leq n$ ）个节点 $a_1, a_2, ..., a_k$ 和 $k$ 条通道，使得对于所有的 $1 \leq i \leq k$ ，都存在一条通道连接节点 $a_i$ 和节点 $a_{(i \bmod k)+1}$ 。闭环的长度为环内所有通道的总长度。

输入描述

第一行包含两个整数 $n$ 和 $m$ （ $3 \leq n \leq 10^5，1 \leq m \leq 10^5$ ），表示原始网络中的节点数和通道数。 接下来的 $m$ 行，每行包含两个整数 $u_i$ 和 $v_i$ （ $1 \leq u_i，v_i \leq n$ ），表示长度为 $2^i$ 的通道连接节点 $u_i$ 和 $v_i$ 。网络中不存在自环或多重通道。需要注意的是，网络并不一定是连通的。

输出描述

每个测试用例输出一行。如果网络中不存在闭环，输出“ $-1$ ”（不带引号）；否则，按照递增顺序输出 $k$ 个整数，用空格分隔，表示最短闭环中的通道的索引。可以证明最多只有一个答案。

样例输入

2
6 8
1 2
2 3
5 6
3 4
2 5
5 4
5 1
4 2
4 2
1 2
4 3

样例输出

2 4 5 6
-1

说明

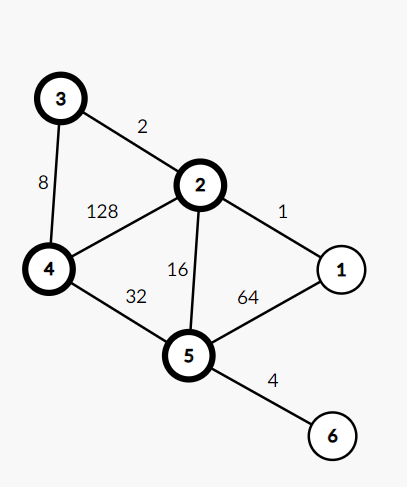
标黑点所围成的闭环是最短的闭环。