### 问题描述 给定 $N$ 个节点 $\frac{N(N-1)}{2}$ 条边的有向图，保证对于每个二元点对 $1 \leq i < j \leq N$，图中一定存在有向边 $(i,j)$ 或 $(j,i)$。现在有 $Q$ 次操作，每次给定 $(i,j)$，翻转边 $(i,j)$ 的方向，即如果存在边 $(i,j)$，将其修改为 $(j,i)$，如果存在边 $(j,i)$，将其修改为 $(i,j)$，随后求解有向图中三元环的个数。即求解有多少个无序三元组 $(i,j,k)$，满足图中存在边 $(i,j),(j,k)$ 和 $(k,i)$。 ### 输入格式 第一行包含 $2$ 个正整数 $N,Q$。 之后 $N$ 行，第 $i$ 行给出长度为 $N$ 的字符串 $s_i$，若 $s_{i,j}=0$，表示图中不存在边 $(i,j)$，若 $s_{i,j}=1$，表示图中存在边 $(i,j)$，保证 $s_{i,i}=0$。 之后 $Q$ 行，每行给定 $i,j$，满足 $1 \leq i < j \leq N$，表示一次修改。 ### 输出格式 输出共 $Q$ 行，每行包含一个整数，表示答案。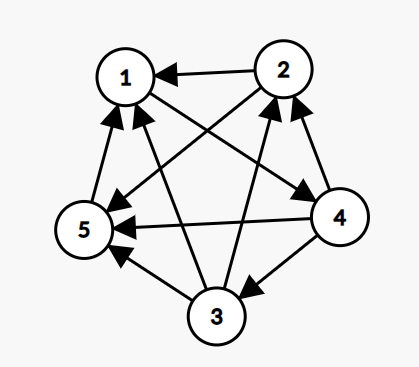 ### 样例输入 ```text 5 1 00000 10001 11001 11101 10000 1 4 ``` ### 样例输出 ```text 3 ``` ### 样例解释 修改后图中存在三元环 $(5,1,4),(3,1,4),(2,1,4)$。  ### 评测数据规模 对于所有测评数据，$1 \leq N \leq 4000,1 \leq Q \leq 10^5$。