### 问题描述 小蓝和小桥在玩一个数学游戏，游戏规则如下： 有一个长度为 $n$ 的 **排列** $a$ 和一个棋子，两个人轮流按照游戏规则在排列上移动这个棋子，**由小蓝先手**，**最先不能移动棋子的人判为输**。 对于某一次移动，设棋子的移动起点为 $i$ ，移动的终点为 $j$，两人移动棋子均需要满足以下游戏规则： 1. $a_i < a_j$。 2. 移动的步长必须是斐波拉契数。在这道题中我们对斐波拉契数的定义为无穷集合 $1, 2, 3, 5, 8 \cdots$，即满足 $f[1]=1, f[2]=2,...,f[n]=f[n-1]+f[n-2]$。 3. 棋子每次走的步长需满足递增关系。假设上一次移动是从 $i'$ 到 $j'$，那么需要满足关系 $|i-j| >|i'-j'|$。 现在小蓝和小桥要进行 $n$ 轮游戏，第 $i$ 轮棋子的初始位置在 $i$（$1\le i\le n$）。对于每一轮游戏，在双方都采用最佳策略的情况下，你需要确定谁将获胜。请注意，棋子的移动是有限的，意味着最终总会有一方获胜。 排列：对于一个长度为 $n$ 的序列，其中 $1\sim n$ 均出现一次。 ### 输入格式 第 $1$ 行输入一个正整数 $n$，代表小蓝和小桥拥有的排列的长度。 第 $2$ 行输入 $n$ 个正整数，表示 $a_1,a_2,…,a_n$ 排列中的每个数。 ### 输出格式 输出 $n$ 行字符串，第 $i(1\le i\le n)$ 个字符串表示：棋子初始位置为 $i$，如果小蓝必胜有必胜的方式，则输出 "Little Lan"，如果小桥有必胜的方式，则输出 "Little Qiao"。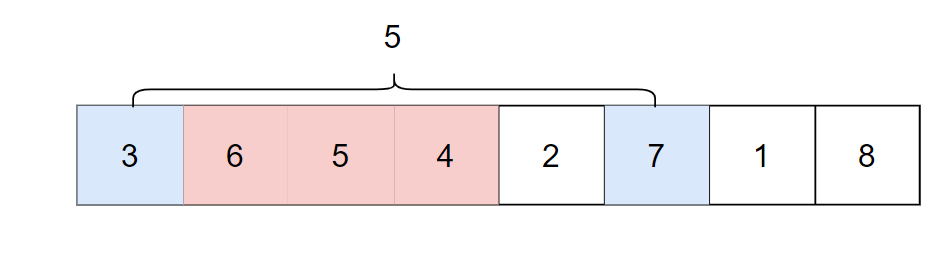 ### 样例输入1 ```text 8 3 6 5 4 2 7 1 8 ``` ### 样例输出1 ```text Little Lan Little Qiao Little Lan Little Lan Little Lan Little Lan Little Lan Little Qiao ``` ### 说明 对于样例 $1$，开始时，小蓝在 $1$ 号位置，他选择斐波拉契数 $5$ 为移动距离，移动棋子到第 $6$ 个位置，该位置上的数为 $7$，则下个回合小桥无法移动棋子，小蓝胜。 红色部分为小蓝可以选择移动的位置，第一个蓝色部分为小蓝的起点，第二个蓝色部分为小蓝选择可以先手必胜的位置。  ### 评测数据规模 对于 $100$% 的评测数据，$1 \leq n \leq 100000$，$1 \leq a_i \leq n$。 此外，不存在一对索引 $i \neq j$ 使得 $a_i = a_j$。