### 问题描述 有 $n$ 个传送阵，编号为 $1\sim n$，每个传送阵使用若干块 "星石" 作为能源。"星石" 是一种很神奇的物质，一块 "星石" 的 **能量值等于它的价值**。同时，星石放在一起会激发更强大的能量，例如：有 $3$ 块 "星石" 的能量值分别为 $2,3,4$，则它们放在一起可以提供的能量为 $2\times 3\times4=24$，需要消耗的价值为 $2+3+4=9$。 现在每个传送阵都有一个能量值 $x$， $f(x)$ 是构成 $x$ 的星石最小价值之和对 $n$ 取模加一，换句话说便是 $f(x)=(\text{sum}\bmod n)+1$，$\text{sum}$ 是构成 $x$ 的星石最小价值之和。 例如： $x=9,n=997,f(x)=(3+3)\bmod 997+1=7$。 而两个传送阵可以相互传送的规则如下： 1. 如果两个传送阵的 $f(x)$ 相等，则两个传送阵可以相互传送。例如 $n>6,x=8,x=9$ 便可以相互传送。 2. 能量值为 $x$ 的传送阵可以和 **编号** 为 $f(x)$ 的传送阵相互传送。例如 $n>6,a[4]=9$（$a[4]$ 是假设 $4$ 号传送阵能量为 $9$），所以 $4$ 号传送阵可以和 $7$ 号传送阵能相互传送。因为 $4$ 号传送阵的能量值为 $9$，$f(x)=(3+3 \bmod n) +1=7$。 给定每个传送阵都有的能量值 $x$，你需要求出从编号 $a$ 到编号 $b$ 的最少传送次数，若不能到达，请输出 $\text{-}1$。 ### 输入格式 第 $1$ 行输入 $3$ 个正整数，表示 $n,a,b$，含义为传送阵的数量，起点编号与终点编号。 第 $2$ 行输入 $n$ 个正整数 $x$，表示每个传送阵的能量值。 ### 输出格式 输出 $1$ 行，表示 $a$ 到 $b$ 的最少传送次数，若不能从 $a$ 传送到 $b$ 则输出 $\text{-}1$。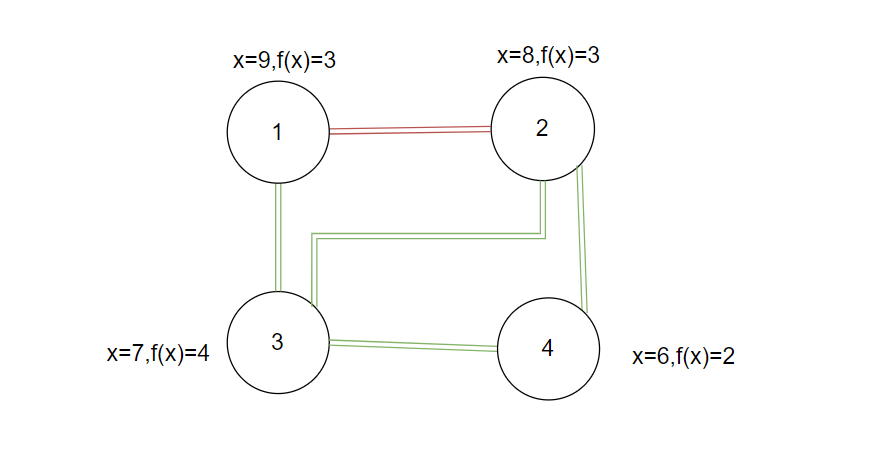 ### 样例输入 ```text 4 1 4 9 8 7 6 ``` ### 样例输出 ```text 2 ``` ### 说明 形成的图如下所示：  红色线为 $f(x)$ 相同互相连接，绿色的线为编号为 $f(x)$ 互相连接。 $1$ 号点到 $4$ 号点可以 $1\rightarrow 3\rightarrow 4,1\rightarrow 2\rightarrow 4$，有二种方式可以到达 $4$ 号点，均是最优路径走法。 ### 评测数据规模 $2\le n \le 10^5,2\le x\le10^8,1\le a,b\le n$。