### 问题描述 在数学王国中，存在一个大小为 $N \times M$ 的神秘迷宫。第 $i$ 行第 $j$ 个位置坐标为 $(i,j)$，每个位置 $(i, j)$ （$1 \leq i \leq N, 1 \leq j \leq M$）都对应着一个正整数 $A_{i, j}$。迷宫的左上角坐标为 $(1,1)$，右下角坐标为 $(N,M)$。 小蓝初始位于坐标 $(1, 1)$，并携带着 $Q$ 把密匙。他的目标是移动到迷宫的终点，即坐标 $(N, M)$ 处。但是通往迷宫尽头的道路并不是一帆风顺的，在前进的过程中，他遇到了一些奇特的规则。 规则如下： 1. 小蓝每次只能向右移动一个位置或向下移动一个位置。 2. 当小蓝所在位置的数和下一步移动位置的数**互质**时，会有一扇封闭的铁门，小蓝需要消耗一把密匙来打开铁门，打开铁门后，这把钥匙将被摧毁。如果没有密匙，小蓝将无法移动到该位置。 你需要输出小蓝从起点到终点路径之和的最大值，如果无法从起点到达终点，输出 `-1`。 ### 输入格式 第一行输入包含 $3$ 个整数 $N, M, Q$，分别为迷宫的大小和密匙的数量。 接下来输入 $N$ 行，每行 $M$ 个整数，为迷宫上的数值 。 ### 输出格式 输出仅一行，包含一个整数，表示答案。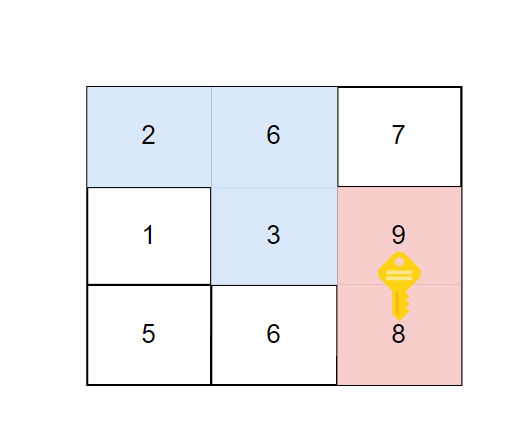 ### 样例输入 ```text 3 3 1 2 6 7 1 3 9 5 6 8 ``` ### 样例输出 ```text 28 ``` ### 说明 对于样例，最优路径关系如下：  在 $9\rightarrow 8$ 时消耗了一把钥匙。 ### 评测数据规模 $1 \leq N, M \leq 1000$。 $0 \leq Q \leq 3$。 $1 \leq A(i, j) \leq 10^9$。