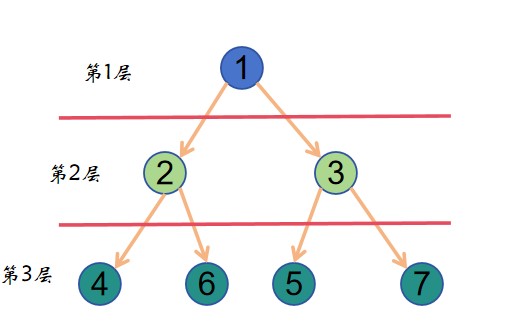
### 问题描述 小蓝和小桥上完课后，小桥回顾了课上教的树形数据结构，他在地上画了一棵根节点为 $1$ 的树，并且对每个节点都赋上了一个权值 $w_i$。 小蓝对小桥多次询问，每次询问包含两个整数 $x, k$，表示询问节点为 $x$ 的所有 $k$ 层子节点中，最大值是多少。 我们称节点 $v$ 为 $x$ 的 $k$ 层子节点满足： 1. $v$ 是 $x$ 为根的子树中的节点。 2. $dep_v - dep_x = k$，$dep_v$ 为 $v$ 在树中的深度。 例如：  $\lbrace 2,3 \rbrace$ 为 $1$ 号点的 $1$ 层子节点，$\lbrace 4,5,6,7 \rbrace$ 为 $1$ 号点的 $2$ 层子节点，$\lbrace 4,6 \rbrace$ 为 $2$ 号点的 $1$ 层子节点。 ### 输入格式 第一行输入两个正整数 $n,q$，表示树的节点数量和询问数量。 第二行输入 $n$ 个正整数 $w_1,w_2,...,w_n$，表示每个点的权值。 接下来 $n-1$ 行，每行输入两个整数 $v_i,u_i$，表示存在一条由 $v_i$ 指向 $u_i$ 的边。 接下来 $q$ 行，每行输入两个整数 $x,k$，表示询问 $x$ 的 $k$ 层子节点中，最大值是多少。 ### 输出格式 输出 $q$ 行，每行输出一个整数，表示每个询问的最大值。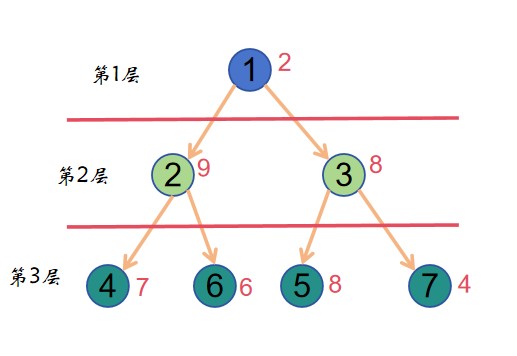 ### 样例输入 ``` 7 4 2 9 8 7 8 6 4 1 2 1 3 2 4 2 6 3 5 3 7 1 2 1 1 3 1 2 1 ``` ### 样例输出 ``` 8 9 8 7 ``` ### 说明 样例如下图：  ### 评测数据范围 $1 \le v_i,u_i,k, x\le n \le 10^5, 1 \le w_i \le 10^9, 1 \le q \le 10^5$。 数据保证是一棵以 $1$ 为根的有向树，并且每次询问的 $k$ 一定合法。