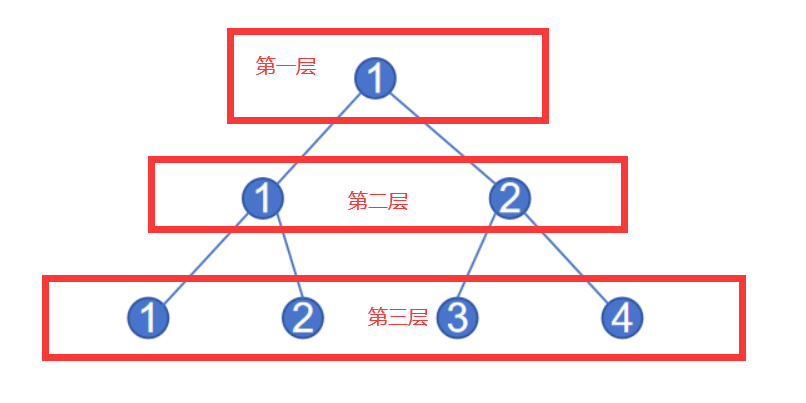
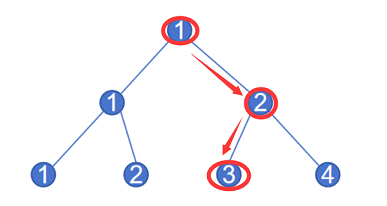
### 问题描述 小蓝最近学了二叉树，他想到了一个问题。 给定一个层数为 $n$ 的满二叉树，每个点编号规则如下：  具体来说，二叉树从上向下数第 $p$ 层，从左往右编号分别为： $1,2,3,4...2^{p-1}$ 。 小蓝给你一条从根节点开始的路径，他想知道到达的节点编号是多少。 例如：路径是 $right-left$ ，那么到达的节点是 $1-2-3$ ，最后到了三号点，如下图所示。  ### 输入格式 第一行输入两个整数 $n,q$ ，$n$ 表示完全二叉树的层数，$q$ 代表询问的路径数量。 接下来 $q$ 行，每行一个字符串 $S$ ，$S$ 只包含字符 { `'L','R'` }，`'L'` 代表向左，`R` 代表向右。 ### 输出格式 输出 $q$ 行，每行输出一个整数，代表最后到达的节点编号。 ### 样例输入 ``` 3 6 R L LL LR RL RR ``` ### 样例输出 ``` 2 1 1 2 3 4 ``` ### 说明 $2 \le n \le 20, 1 \le q \le 10^3, 1 \le |S| \lt n$。 **完全二叉树**：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为 $K$ ，且节点总数是 $2^k-1$ ，则它就是满二叉树。