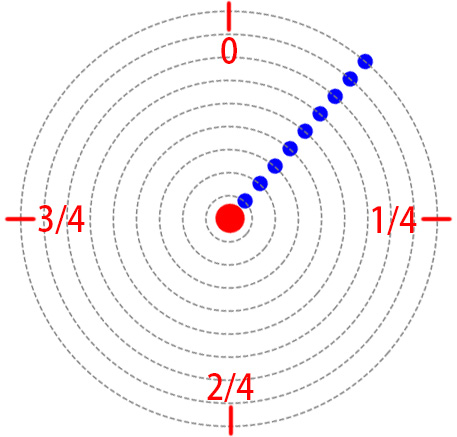
### 问题描述 在一个遥远的星系，有九颗行星围绕着中央的恒星公转。每个行星的公转周期 $t$ 可能不同，且公转方向也可能不同。当一个行星完成了它的公转周期，它会开始新的一轮公转。 当所有九大行星都位于同一条直线上时，这个星系会发生一个神奇的现象。星系中的智慧生命想知道，为了等待所有行星都位于同一直线上，他们最少需要等待多久。你能帮助他们计算出这个时间吗？ 为了简便计算，我们可以认为九颗行星均是在同一平面上以固定的半径匀速公转的。且只有**所有行星均位于 $0$ 刻度位置**时的九星连珠现象才视为有效。  ### 输入格式 输入共有 $9$ 行，每行包括三个整数 $t_i,a_i, b_i$，其中 $t_i=1$ 表示该行星是以顺时针方向旋转的，即行星刻度是增加的，$t_i=0$ 则表示表示该行星是以逆时针方向旋转的，即行星刻度是减少的。行星的公转周期为 $a_i$ 天，并且初始位置为第 $b_i$ 天。题目保证输入的每个公转周期互质。 ### 输出格式 输出包含一个正整数，表示等待多少天后，所有行星都将位于同一直线上。 ### 样例输入 ``` 0 2 1 0 3 0 1 5 1 0 7 2 1 11 5 1 13 5 0 17 10 0 19 6 1 23 7 ``` ### 样例输出 ``` 41 ``` ### 测评数据规模 $0 \leq b_i < a_i \leq 10^3$，$1 \leq \prod a_i \leq 10^{18}$。