### 问题描述 笛卡尔树模板题。 笛卡尔树是一种二叉树，每一个结点由一个键值二元组 $(k,w)$ 构成。要求 $k$ 满足二叉搜索树的性质，而 $w$ 满足堆的性质。如果笛卡尔树的 $k,w$ 键值确定，且 $k$ 互不相同，$w$ 互不相同，那么这个笛卡尔树的结构是唯一的。 当我们把数组元素值当作键值 $w$，把数组下标当作键值 $k$ 来构建笛卡尔树，该笛卡尔树的任意一棵子树内的下标是连续的一个区间，在算法竞赛中有较为广泛的应用。 给定长度为 $n$ 的**排列** $a_1,a_2,...,a_n$，将该排列建成元素值满足大根堆性质（元素值作为 $w$）、下标满足二叉搜索树性质（下标作为 $k$）的笛卡尔树。按 $k$ 从小到大的顺序输出笛卡尔树上每个结点的左右子结点的 $k$ 值，不存在某子节点则在对应位置输出 `0`。 ------ 一个长度为 $n$ 的排列是指将 $1$ 到 $n$ 之间共 $n$ 个互不相同的正整数以任意顺序摆放形成的数组。例如 $[2,3,1,5,4]$ 是一个排列，但 $[1,2,2]$ 不是一个排列（$2$ 在数组中出现了两次），$[1,3,4]$ 也不是一个排列（$n=3$ 但在数组中有 $4$）。 ### 输入格式 第一行，一个正整数 $n(1 \le n \le 2\times10^5)$，表示排列的长度。 第二行，$n$ 个正整数 $a_1,a_2,\dots,a_n$，表示给定排列。 ### 输出格式 共 $n$ 行，第 $i$ 行包括两个整数 $l_i,r_i$，表示笛卡尔树上 $k=i$ 的结点的左右子节点的 $k$ 值。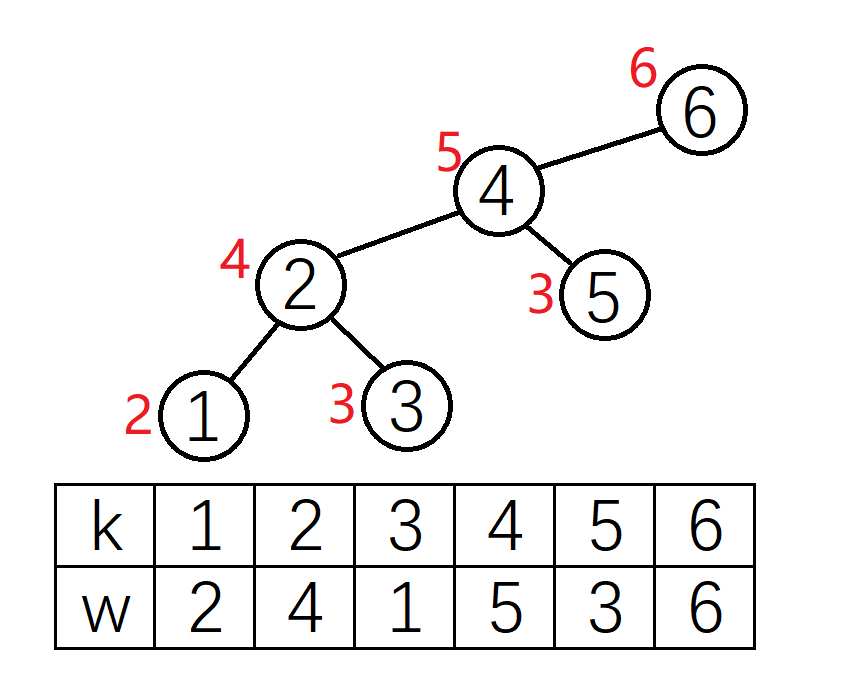 ### 样例输入 ```text 6 2 4 1 5 3 6 ``` ### 样例输出 ```text 0 0 1 3 0 0 2 5 0 0 4 0 ``` ### 说明  ### 评测数据规模 $1\le n \le 2\times 10^5,1\le a_i\le 2\times 10^5$。