### 问题描述 小秋最近在研究树上问题。一天他在对着一颗树发呆的时候，想到了一个神奇的题目。 给定一颗包含 $n$ 个顶点的树，每个点权为 $w_i$，每条边边权 $c_i$。现在需要你完成 $q$ 次操作，操作分为以下四种。 1. 给定树上两个不同的点 $a,b$ 和一个整数 $x$，将 $a,b$ 两点的路径上的所有边权都异或上 $x$。 2. 给定树上两个不同的点 $a ,b$ 和一个整数 $x$，将 $a,b$ 两点的路径上的所有点权都异或上 $x$。 3. 给定树上两个不同的点 $a,b$，求 $a, b$ 两点的路径上所有点权的异或和。 4. 给定树上一个点 $a$，求 $a$ 的点权和与 $a$ 相连所有边的边权的异或和。 ### 输入格式 第一行包含两个整数 $n,q$，分别表示树的顶点个数、操作的总个数。 第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 个顶点的初始点权 $w_i$。 接下来 $n - 1$ 行，每行输入三个整数，格式 `u v c`，第 $i$ 行表示有一条连接 $u_i,v_i$ 边权为 $c_i$ 的边。 接下来 $q$ 行每行包含若干个整数，表示一个操作，具体如下： 操作 $1$：格式：`1 a b x` 含义：将 $a,b$ 两点的最短路径上的所有边权都异或上 $x$。 操作 $2$：格式：`2 a b x` 含义：将 $a,b$ 两点的最短路径上的所有点权都异或上 $x$。 操作 $3$：格式：`3 a b` 含义：求 $a, b$ 两点的最短路径上所有点权的异或和。 操作 $4$：格式：`4 a` 含义：求 $a$ 的点权和与 $a$ 相连所有边的边权的异或和。 注：本题输入数据较大，建议采用较快的数据读入方式。 ### 输出格式 输出包含多行，对于 $3,4$ 操作，输出一行，包含一个整数，表示当前操作的答案。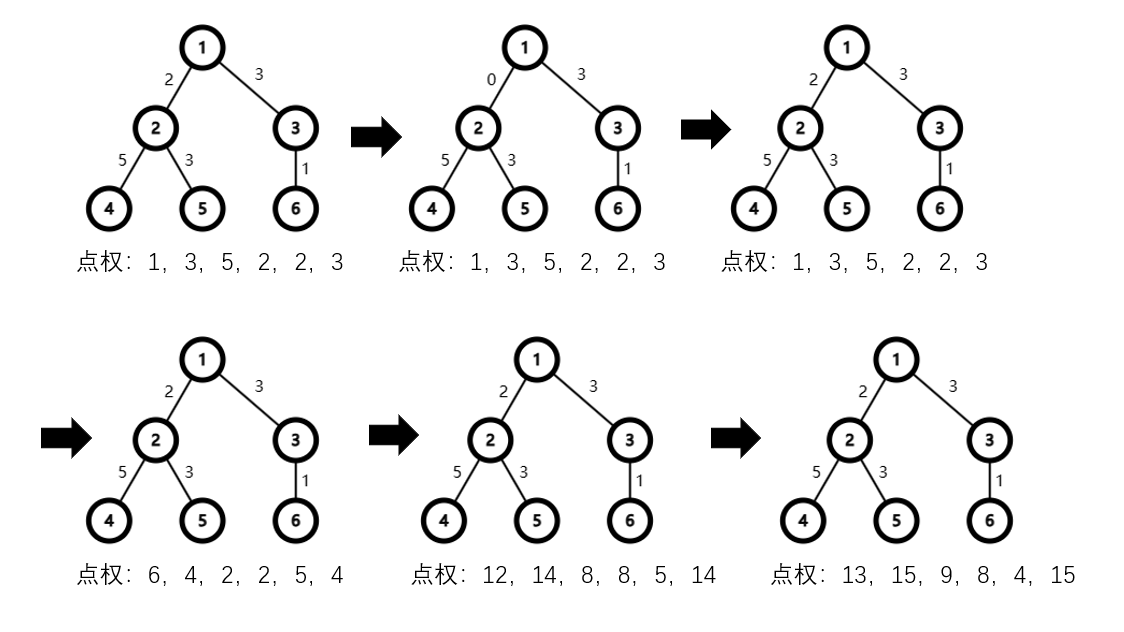 ### 样例输入 ``` 6 10 1 3 5 2 2 3 1 2 2 1 3 3 2 4 5 2 5 3 3 6 1 1 1 2 2 1 2 1 2 3 1 5 4 3 2 5 6 7 3 2 6 2 4 6 10 4 5 2 5 6 1 3 5 6 ``` ### 样例输出 ``` 0 7 4 6 0 ``` ### 说明 几次修改操作树的变化如下：  ### 评测数据规模 对于 $20$% 的评测数据，$1 \leq n,q \leq 10^3$； 对于 $40$% 的评测数据，$1\leq n,q \leq 10^4$； 对于 $100$% 的评测数据，$1 \leq n,q \leq 10^5 , 0 \leq w_i,c_i,x \leq 10^9$。