### 问题描述 在水平数轴上有 $N$ 条线段，每条线段用 $(l_i,r_i)$ 表示（其中，$l_i$ 代表线段的左端点，$r_i$ 代表线段的右端点，且都为整数）。 现在给定一个正整数 $k$，规定每次可以在数轴上对任意 $[t,t+k-1]$ 区间进行染色操作，**使得与该区间有重叠的线段都被染成黑色**。 问：最少需要操作多少次，使得这 $N$ 条线段都被染成黑色。假设开始时，所有线段都不是黑色。 ### 输入格式 输入第 $1$ 行包含两个正整数 $N$ 和 $k$，分别表示线段的数量和给定的整数。 第 $2\sim N+1$ 行每行两个正整数 $l_i,r_i$，表示每条线段的左右端点。 ### 输出格式 输出仅一行，包含一个整数，表示答案。 ### 样例输入1 ```text 3 3 1 2 3 7 5 9 ``` ### 样例输出1 ```text 2 ``` ### 样例输入2 ```text 3 3 1 2 4 7 4 9 ``` ### 样例输出2 ```text 1 ``` ### **说明/提示** 对于所有评测数据，$1\leq N\leq 2\times 10^5，1\leq k\leq 10^9,1\leq l_i\leq r_i\leq 10^9$。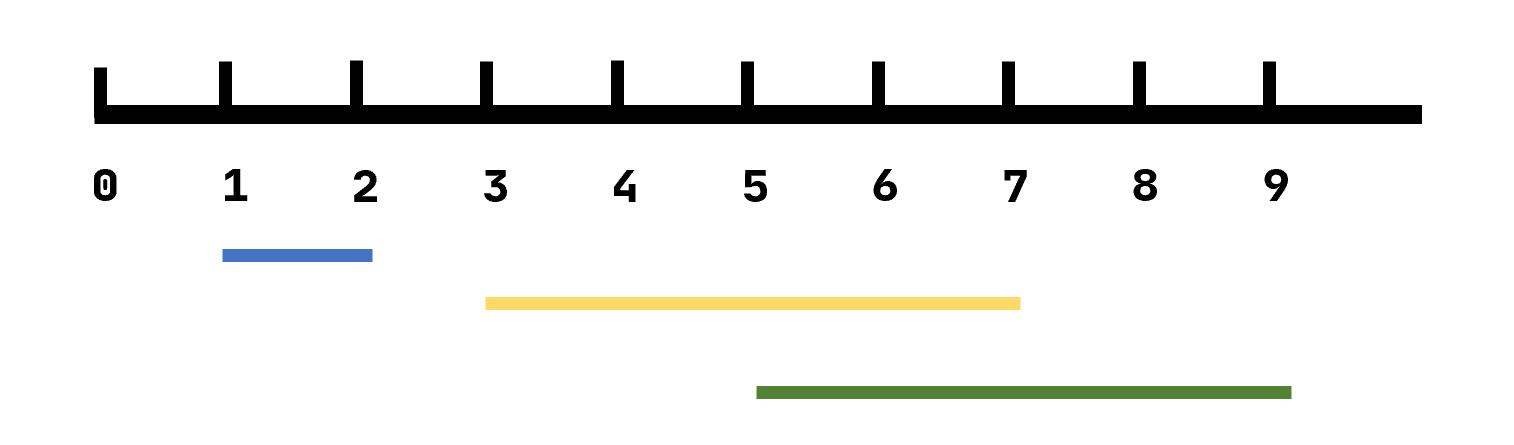 样例 $1$ 中，线段分布如下图所示：  第一次可以选取区间 $[2,4]$，将线段 $1$ 和 $2$ 染成黑色； 第二次可以选取区间 $[6,8]$，将线段 $2$ 和 $3$ 染成黑色。 经过验证，最少需要 $2$ 次操作才能使得这三条线段全部被染成黑色，因此答案 $=2$。