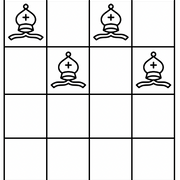
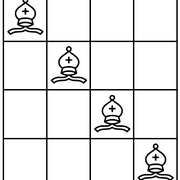
### 问题描述 小浩有一个大小为 $N\times N$ 的国际象棋棋盘。 有 $N$ 个主教以之字形的形式放置在棋盘的矩阵上，坐标分别为 $(1,1),(2,2),(1,3),(2,4),(1,5),\dots​$。 例如对于 $N=4​$，棋盘初始时为：  已知主教只能斜向移动且每次可以移动任意距离。 你的任务是找到最少的移动次数，满足对于所有 $1\le i\le N$，棋盘矩阵上的格子 $(i,i)​$ 都被主教占领了。 对于 $N=4​$，最后的位置应该为：  ### 输入格式 第一行输入一个正整数 $T$ 表示测试数据的组数。 接下来 $T$ 行每行输入一个正整数 $N$ 表示棋盘的大小。 ### 输出格式 对于每组测试数据，输出一个整数表示满足题目要求所需要的最少的移动次数，并换行。 ### 样例输入1 ```text 4 1 4 2 6 ``` ### 样例输出1 ```text 0 3 0 6 ``` ### 说明 样例 $1$：棋盘的主教一开始已经处于最终位置了。 样例 $2$： 我们最少需要 $3$ 次移动： - 将主教从 $(2,2)$ 移动到 $(4,4)$。 - 将主教从 $(1,3)$ 移动到 $(2,2)$。 - 将主教从 $(2,4)$ 移动到 $(3,3)$。 样例 $3​$：棋盘的主教一开始已经处于最终位置了。 ### 评测数据规模 对于所有的评测数据，$1\le T \le 2\times10^5$，$1\le N\le10^9$。