### 问题描述 Alice 与 Bob 玩腻了取数游戏，于是他们发明了一种新的游戏，取名为取树游戏。 游戏在一个有根树上进行。树上共有 $n$ 个节点，按照 $1$ 到 $n$ 的顺序编号，$1$ 号节点为根节点。 游戏开始后，玩家轮流进行操作。在每个回合中，当前玩家可以选择任意数量的叶子节点，并将其删去。当某个玩家无法进行操作时，他就输掉了游戏。换句话说，删去最后一个节点的玩家将取得胜利。 注意： - 叶子节点是指那些没有子节点的节点，当根节点失去其所有子节点后也会成为叶子节点。 - 每回合中，玩家必须删去至少一个叶子节点。 Alice 先进行操作。Alice 和 Bob 都很聪明，他们都会采取最优策略进行游戏。请你确定游戏的获胜者。 ### 输入格式 每个测试输入包含多个测试用例。输入的第一行包含一个正整数 $t$ ($1\le t\le 10^5$)，表示测试用例的组数。测试用例的描述如下： 每个测试用例的第一行包含一个整数 $n$ ($1\le n\le 10^5$)，表示树上节点的数量。 测试用例的第二行包含 $n-1$ 个正整数 $a_2, a_3, \ldots, a_n$ ($1\le a_i\lt i, 2\le i\le n$)，其中 $a_i$ 表示节点 $i$ 的父节点是 $a_i$。 容易证明，输入数据保证构成一棵 $1$ 号节点为根节点的有根树。 数据保证，所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。 ### 输出格式 对于每个测试用例，输出的唯一一行包含一个字符串，表示游戏的获胜者。如果 Alice 获胜，则输出 `Alice`；如果 Bob获胜，则输出 `Bob`。 ### 样例输入 ```text 4 5 1 1 1 1 4 1 2 3 5 1 2 1 4 5 1 2 3 2 ``` ### 样例输出 ```text Alice Bob Bob Alice ``` ### 说明 考虑第一个测试用例。 初始状态下树的形状如下图所示。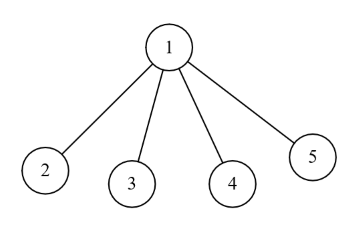  此时 Alice 只需要删去 $3$、$4$、$5$ 号节点，便能获胜，得到的树如下图所示。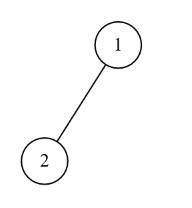  此时 Bob 只能删去 $2$ 号节点，如下图所示。  因此 Alice 删去最后一个节点，获得胜利。