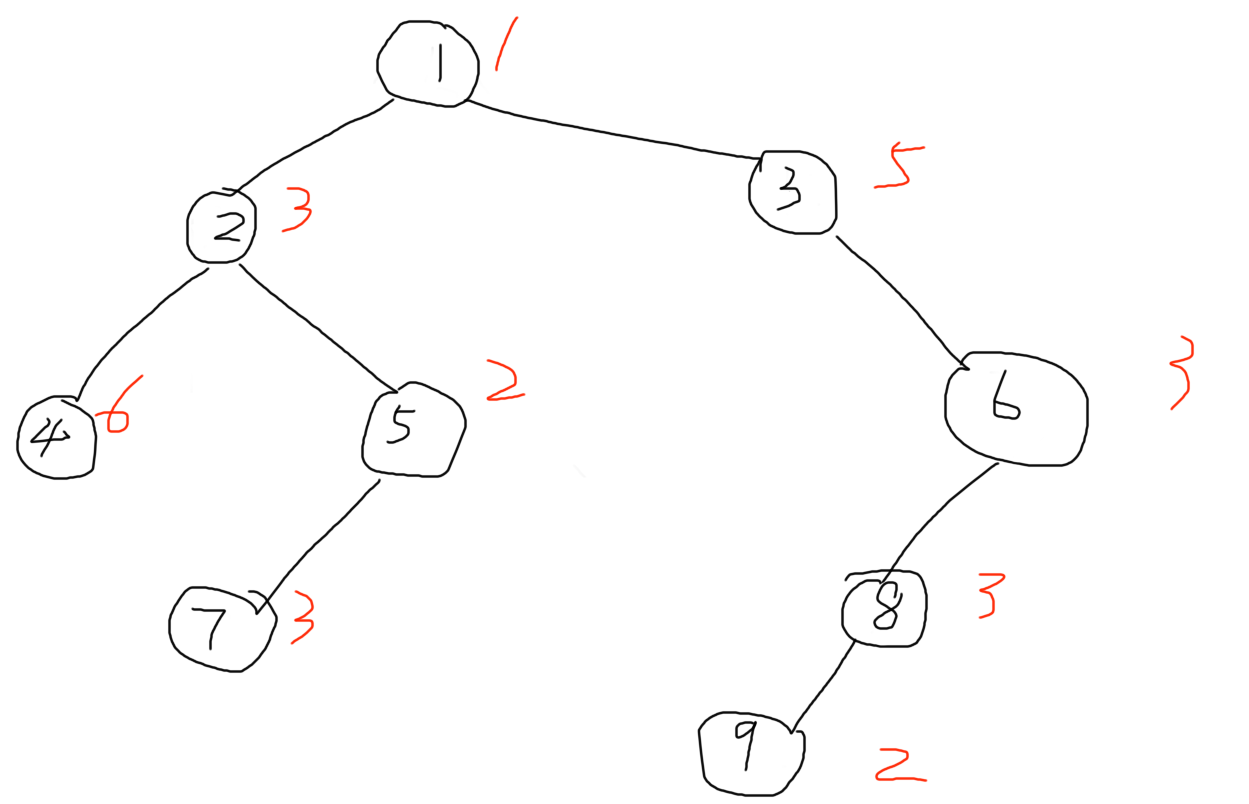
### 问题描述 给定一棵 $n$ 个点 $n - 1$ 条边的二叉树，编号为 $1, 2, \dots, n$，其中 $1$ 号点为根节点，其中第 $i$ 个点的权重为 $w_i$。 请你计算出这棵树的 **黄金指数** 为 $0$ 的点的权重之和。 **黄金指数**： - 若一个点是它父节点的左儿子，则它的黄金指数为其父节点的黄金指数 $+1$。 - 若一个点是它父节点的右儿子，则它的黄金指数为其父节点的黄金指数 $-1$。 - 特别的，根节点的黄金指数为 $0$。 ### 输入格式 第一行输入一个正整数 $n$，表示树中点的数量。 第二行输入 $n$ 个正整数 $w_1, w_2, \dots, w_n$，$w_i$ 表示 $i$ 点的权重。 接下来 $n$ 行，每行两个整数 $l_i, r_i$，其中第 $i$ 行表示 $i$ 点的左儿子与右儿子，若为 `-1` 则表示不存在。 ### 输出格式 一行一个一个整数，表示这棵树的 **黄金指数** 为 $0$ 的点的权重之和。 ### 样例输入 ``` 9 1 3 5 6 2 3 3 3 2 2 3 4 5 -1 6 -1 -1 7 -1 8 -1 -1 -1 9 -1 -1 -1 ``` ### 样例输出 ``` 5 ``` ### 数据范围 对于 $100$% 的数据，$1 \leq n \leq 10^5$，$1 \leq w_i \leq 10^3$，$l_i, r_i \in [1, n]$ $\cup$ {$-1$}。