### 问题描述 小蓝有一天误入了一个混境之地。 好消息是：他误打误撞拿到了一张地图，并从中获取到以下信息： 1. 混境之地的大小为 $n \cdot m$，其中 `#` 表示这个位置很危险，无法通行，`.` 表示道路，可以通行。 2. 他现在所在位置的坐标为 $(A, B)$ ，而这个混境之地出口的坐标为 $(C, D)$ ，当站在出口时即表示可以逃离混境之地。 3. 混境之地中有 $k$ 个单向传送门，当你站在上面时，你可以选择消耗 $p_i$ 点能量，从当前点 $(x1_i, y1_i)$ 传送至 $(x2_i, y2_i)$ ，同样你也可以选择不通过该传送门。 坏消息是：小蓝仅剩下 $E$ 点能量。 小蓝可以往上下左右四个方向行走，每行走一步，消耗一点能量。 小蓝想知道他能否逃离这个混境之地，如果可以逃离这里，请你帮他计算一下，他最多可以剩下多少能量，如果无法逃离则输出 `-1` 。 ### 输入格式 第 $1$ 行输入两个正整数 $n, m$ ，表示混境之地的大小。 第 $2$ 行输入四个正整数 $A, B, C, D$ ，表示小蓝当前所在位置的坐标，以及混境之地出口的坐标。 第 $3$ 行至第 $n + 2$ 行，每行 $m$ 个字符，表示混境之地的地图，其中 `#` 表示为危险的地方， `.` 表示普通的道路。 第 $n + 3$ 行输入一个正整数 $k$ ，表示传送门的数量。 接下来 $k$ 行，每行五个正整数 $x1_i, y1_i, x2_i, y2_i, p_i$ ，表示 $(x1_i, y1_i)$ 处有一个单项传送门，可以消耗 $p_i$ 点能量使用该传送门从 $(x1_i, y1_i)$ 传送至 $(x2_i, y2_i)$ 。 最后一行输入一个 $E$ ，表示小蓝剩下的能量值。 ### 输出格式 输出数据共一行为一个整数： - 若小蓝可以逃离混境之地，则输出他最多可以剩下的能量值。 - 若小蓝无法逃离混境之地，则输出 `-1` 。 ### 样例输入1 ```txt 5 5 1 1 2 5 ...#. ..#.. #...# ...#. ..... 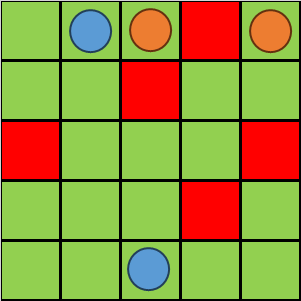2 1 2 5 3 1 1 3 1 5 2 7 ``` ### 样例输出1 ```txt 2 ``` ### 样例解释1  如图所示，绿色方块表示普通道路，红色方块表示危险的地方，蓝色圆圈为传送门 $1$ ，橙色圆圈为传送门 $2$ 。 从 $(1, 1)$ 到 $(2, 5)$ 的最短道路为： $(1, 1) -> (1, 2) -> (1, 3) -> (1, 5) -> (2, 5)$ ，共消耗 $5$ 点能量，由于起始能量为 $7$ ，故剩余 $2$ 点能量。 ### 样例输入2 ```txt 5 5 1 1 2 5 ...#. ..#.. #...# ...#. ..... 2 1 2 5 3 1 1 3 1 5 2 4 ``` ### 样例输出2 ```txt -1 ``` ### 样例解释2 如样例 $1$ 所示，从 $(1, 1)$ 到 $(2, 5)$ 最少需要 $5$ 点能量，所以无法逃离混境之地，故输出 `-1` 。 ### 数据范围 对于所有测试样例， $1 \leq n, m \leq 50$ ， $1 \leq A, C, x1_i, x2_i \leq n$ ， $1 \leq B, D, y1_i, y2_i \leq m$ ， $0 \leq k \leq n \times m$ ， $1 \leq p_i \leq 10^6$ ， $0 \leq E \leq 10^6$ 。 数据保证，传送门的启动点和到达点均为普通道路，且一个点只能是一个传送门的启动点，但一个点可以是多个传送门的到达点。