### 问题描述 给定一棵树，树中包含 $n$ 个结点，编号为 $1\sim n$ ，以及 $n-1$ 条无向边，每条边都有一个权值。 现从树中任选一个点，从该点出发，在不走回头路的情况下找出二条到其他点的路径，这二条路径不能有公共边，请问这二条路径长度的乘积最大可以是多少。 注：如果从该点出发只有一个方向可以走，换句话说该点入度出度为 $1$，则乘积为 $0$ 。 ### 输入格式 第一行输入一个整数 $n$。 接下来 $n-1$ 行，每行输入包含三个整数 $a_i,b_i,c_i$，表示点 $a_i$ 和 $b_i$ 之间存在一条权值为 $c_i$ 的边。 ### 输出格式 输出一个整数，为二条路径长度乘积的最大值。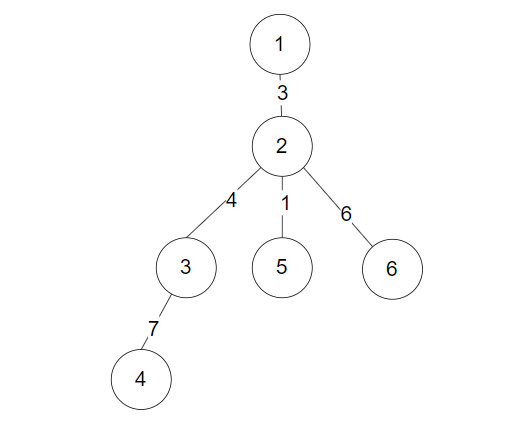 ### 样例输入 ```text 6 1 2 3 2 3 4 3 4 7 2 5 1 2 6 6 ``` ### 样例输出 ``` 70 ``` ### 说明 样例图为：  从 $1,4,5,6$ 号点出发没有二条路径，$2$ 号点出发的乘积最大为 $(4+7)\times 6=66$，$3$ 号点出发的乘积最大为 $(4+6)\times 7 =70$，因此答案为 $70$。 ### 评测数据规模 $1 \le n \le 10^5,1 \le a_i,b_i \le n,1 \le c_i \le 10^4$。