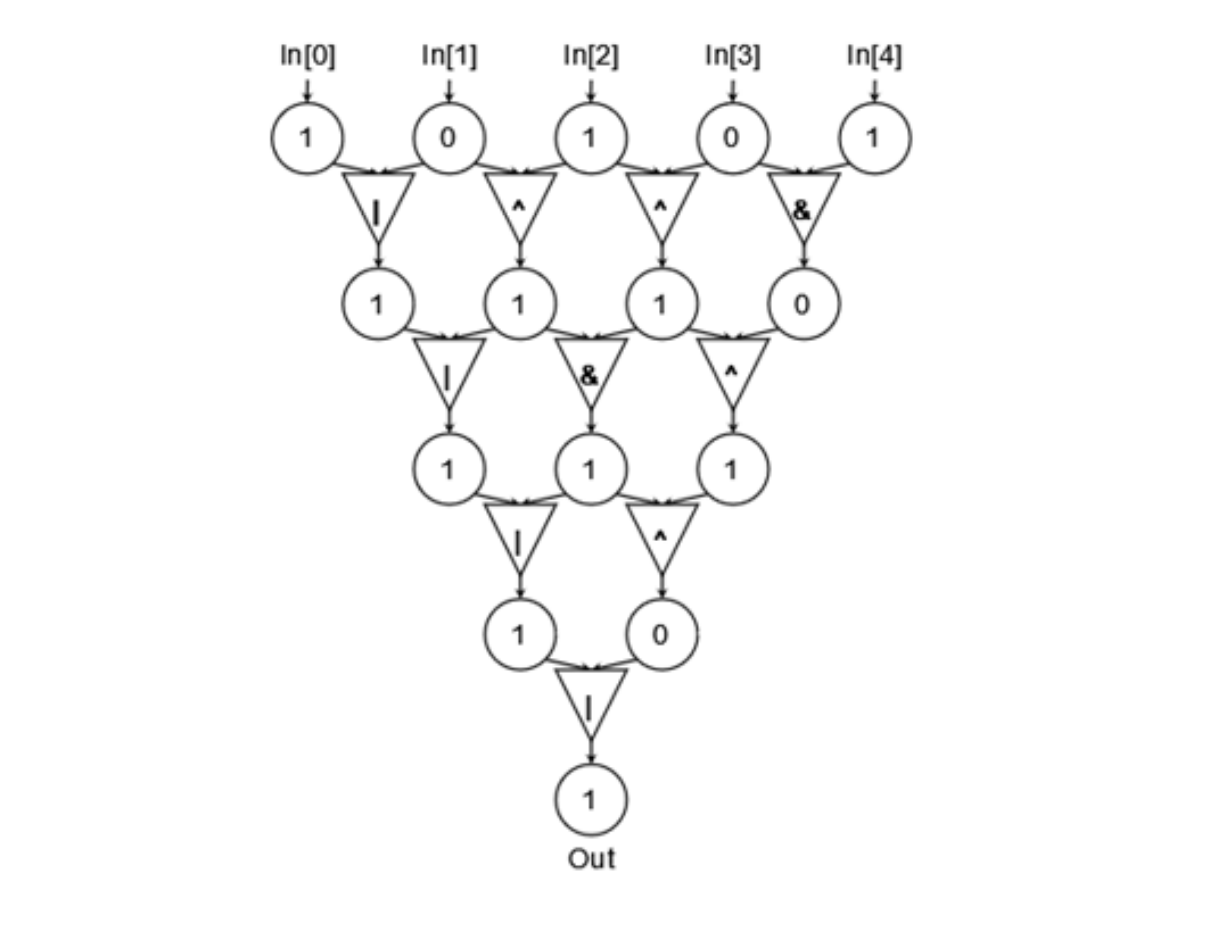
### 问题描述 小蓝有一张门电路的逻辑图，如下图所示：  图中每个三角形代表着一种门电路，可能是与门、或门、异或门中的任何一种，它接受上一层中的两个圆形中的数据作为输入，产生一个输出值输出到 下一级 (如图中箭头所示)。图中圆形表示的是暂存的输出结果，取值只可能是 $0$ 或 $1$，为了便于表示我们用 $\operatorname{arr}[i][j]$ 表示第 $i(0 \leq i \leq 4)$ 行第 $j(0 \leq j \leq i)$ 个圆形的值。其中 $\operatorname{arr}[0]=(\operatorname{In}[0], \operatorname{In}[1], \operatorname{In}[2], \operatorname{In}[3], \operatorname{In}[4])$ 表示的是输入数据，对于某个 $\operatorname{arr}[i][j](i \leq 0)$，计算方式为 $\operatorname{arr}[i][j]=\operatorname{arr}[i-1][j]$ op $\operatorname{arr}[i-1][j+1]$，其中 $o p$ 表示的是将 $\operatorname{arr}[i-1][j]$、$\operatorname{arr}[i-1][j+1]$ 作为输入，将 $\operatorname{arr}[i][j]$ 作为输出的那个门电路, 与门、或门、异或门分别对应于按位与 $(\&) 、$ 按位或 $(1)$ 、按位异或 (^) 运算符。 现在已知输入为 $\operatorname{In}[0]=1, \operatorname{In}[1]=0, \operatorname{In}[2]=1, \operatorname{In}[3]=0, \operatorname{In}[4]=1$，小蓝想要使得最终的输出 $O u t$ 的值为 1， 请问一共有多少种不同的门电路组合方式？其中上图中显示的就是一种合法的方式。 ### 答案提交 这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。