### 问题描述 在桌面从左至右横向摆放着 $N$ 堆石子。每一堆石子都有着相同的颜色，颜色可能是颜色 $0$，颜色 $1$ 或者颜色 $2$ 中的其中一种。现在要对石子进行合并，规定每次只能选择位置相邻并且颜色相同的两堆石子进行合并。合并后新堆的相对位置保持不变，新堆的石子数目为所选择的两堆石子数目之和，并且新堆石子的颜色也会发生循环式的变化。具体来说：两堆颜色 $0$ 的石子合并后的石子堆为颜色 $1$，两堆颜色 $1$ 的石子合并后的石子堆为颜色 $2$，两堆颜色 $2$ 的石子合并后的石子堆为颜色 $0$。本次合并的花费为所选择的两堆石子的数目之和。 给出 $N$ 堆石子以及他们的初始颜色，请问最少可以将它们合并为多少堆石子？如果有多种答案，选择其中合并总花费最小的一种，合并总花费指的是在所有的合并操作中产生的合并花费的总和。 ### 输入格式 第一行一个正整数 $N$ 表示石子堆数。 第二行包含 $N$ 个用空格分隔的正整数，表示从左至右每一堆石子的数目。 第三行包含 $N$ 个值为 $0$ 或 $1$ 或 $2$ 的整数表示每堆石头的颜色。 ### 输出格式 一行包含两个整数，用空格分隔。其中第一个整数表示合并后数目最少的石头堆数，第二个整数表示对应的最小花费。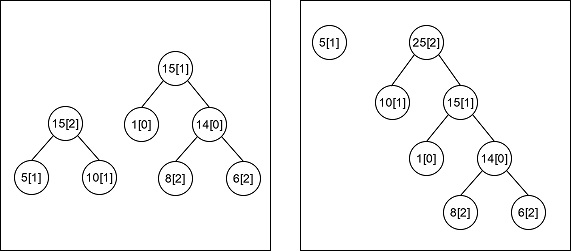 ### 样例输入 ``` 5 5 10 1 8 6 1 1 0 2 2 ``` ### 样例输出 ``` 2 44 ``` ### 样例说明  上图显示了两种不同的合并方式。其中节点中标明了每一堆的石子数目， 在方括号中标注了当前堆石子的颜色属性。左图的这种合并方式最终剩下了两堆石子，所产生的合并总花费为 $15 + 14 + 15 = 44$；右图的这种合并方式最终也剩下了两堆石子，但产生的合并总花费为 $14 + 15 + 25 = 54$。综上所述，我们选择合并花费为 $44$ 的这种方式作为答案。 ### 评测用例规模与约定 对于 $30$% 的评测用例，$1 \leq N \leq 10$。 对于 $50$% 的评测用例，$1 \leq N \leq 50$。 对于 $100$% 的评测用例，$1 \leq N \leq 300, 1 \leq$ 每堆石子的数目 $\leq 1000$。