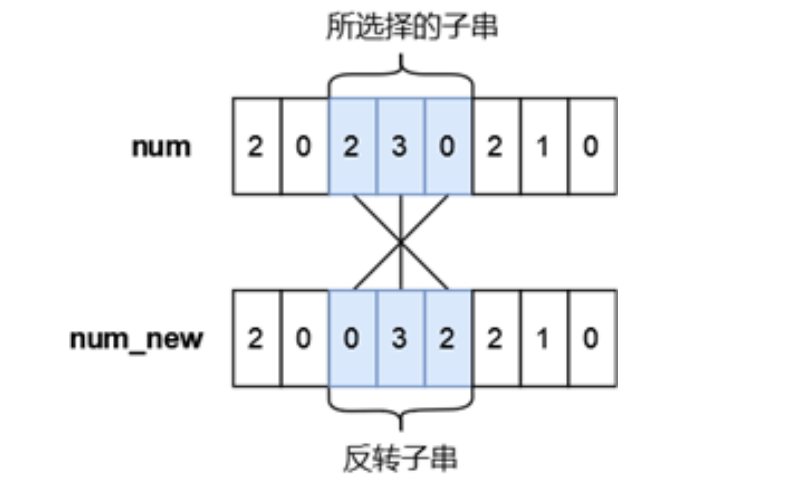
### 问题描述  小蓝有一个长度均为 $n$ 且仅由数字字符 $0 \sim 9$ 组成的字符串，下标从 $0$ 到 $n-1$，你可以将其视作是一个具有 $n$ 位的十进制数字 $\text{num}$，小蓝可以从 $\text{num}$ 中选出一段连续的子串并将子串进行反转，最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 $num_{new}$ 满足条件 $\text{num}_{\text{new}}<\text{num}$，请你帮他计算下一共有多少种不同的子串选择方案，只要两个子串在 $\text{num}$ 中的位置不完全相同我们就视作是不同的方案。 注意，我们允许前导零的存在，即数字的最高位可以是 $0$，这是合法的。 ### 输入格式 输入一行包含一个长度为 $n$ 的字符串表示 $\text{num}$（仅包含数字字符 $0 \sim 9$），从左至右下标依次为 $0 \sim n-1$。 ### 输出格式 输出一行包含一个整数表示答案。 ### 样例输入 ``` 210102 ``` ### 样例输出 ``` 8 ``` ### 样例说明 一共有 $8$ 种不同的方案： 1. 所选择的子串下标为 $0 \sim 1$，反转后的 $\text{num}_{\text{new}}=120102<210102$； 2. 所选择的子串下标为 $0 \sim 2$，反转后的 $\text{num}_{\text{new}}=012102<210102$； 3. 所选择的子串下标为 $0 \sim 3$，反转后的 $\text{num}_{\text{new}}=101202<210102$； 4. 所选择的子串下标为 $0 \sim 4$，反转后的 $\text{num}_{\text{new}}=010122<210102$； 5. 所选择的子串下标为 $0 \sim 5$，反转后的 $\text{num}_{\text{new}}=201012<210102$； 6. 所选择的子串下标为 $1 \sim 2$，反转后的 $\text{num}_{\text{new}}=201102<210102$； 7. 所选择的子串下标为 $1 \sim 4$，反转后的 $\text{num}_{\text{new}}=201012<210102$； 8. 所选择的子串下标为 $3 \sim 4$，反转后的 $\text{num}_{\text{new}}=210012<210102$； ### 评测用例规模与约定 对于 $20$% 的评测用例，$1 \leq n \leq 100$； 对于 $40$% 的评测用例，$1 \leq n \leq 1000$； 对于所有评测用例，$1 \leq n \leq 5000$。