作业调度方案 ### 题目描述 我们现在要利用 $m$ 台机器加工 $n$ 个工件，每个工件都有 $m$ 道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。 每个工件的每个工序称为一个操作，我们用记号 $j-k$ 表示一个操作，其中 $j$ 为 $1$ 到 $n$ 中的某个数字，为工件号；$k$ 为 $1$ 到 $m$ 中的某个数字，为工序号，例如 $2-4$ 表示第 $2$ 个工件第 $4$ 道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。 例如，当 $n=3，m=2$ 时，$“1-1，1-2，2-1，3-1，3-2，2-2”$ 就是一个给定的安排顺序，即先安排第 $1$ 个工件的第 $1$ 个工序，再安排第 $1$ 个工件的第 $2$ 个工序，然后再安排第 $2$ 个工件的第 $1$ 个工序，等等。 一方面，每个操作的安排都要满足以下的两个约束条件。 (1) 对同一个工件，每道工序必须在它前面的工序完成后才能开始； (2) 同一时刻每一台机器至多只能加工一个工件。 另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。 由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为 “1 1 2 3 3 2”。 还要注意，“安排顺序”只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。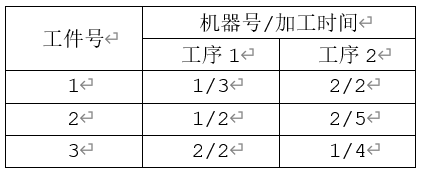 例如，取 $n=3,m=2$，已知数据如下：  则对于安排顺序 “1 1 2 3 3 2”，下图中的两个实施方案都是正确的。但所需要的总时间分别是 10 与 12。  当一个操作插入到某台机器的某个空档时(机器上最后的尚未安排操作的部分也可以看作一个空档)，可以靠前插入，也可以靠后或居中插入。为了使问题简单一些，我们约定：在保证约束条件(1)(2)的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件(1)(2)的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。 显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。 ### 输入描述 第 $1$ 行为两个正整数，用一个空格隔开：$m, n$ (其中 $m(<20)$ 表示机器数，$n(<20)$ 表示工件数)。 第 $2$ 行：$m \times n$ 个用空格隔开的数，为给定的安排顺序。 接下来的 $2n$ 行，每行都是用空格隔开的 $m$ 个正整数，每个数不超过$20$。其中前 $n$ 行依次表示每个工件的每个工序所使用的机器号，第 1 个数为第 1 个工序的机器号，第 2 个数为第 2 个工序机器号，等等。后 $n$ 行依次表示每个工件的每个工序的加工时间。 ### 输出描述 输出一个正整数，为最少的加工时间。 ### 输入输出样例 #### 示例 1 >输入 ```txt 2 3 1 1 2 3 3 2 1 2 1 2 2 1 3 2 2 5 2 4 ``` >输出 ```txt 10 ```