编程题
希尔伯特曲线
### 题目描述
**本题为代码补全填空题,请将题目中给出的源代码补全,并复制到右侧代码框中,选择对应的编译语言(C/Java)后进行提交。若题目中给出的源代码语言不唯一,则只需选择其一进行补全提交即可。复制后需将源代码中填空部分的下划线删掉,填上你的答案。提交后若未能通过,除考虑填空部分出错外,还需注意是否因在复制后有改动非填空部分产生错误。**
希尔伯特曲线是以下一系列分形曲线 $H_n$ 的极限。我们可以把 $H_n$ 看作一条覆盖 $2^n \times 2^n$ 方格矩阵的曲线,曲线上一共有 $2^n \times 2^n$ 个顶点(包括左下角起点和右下角终点),恰好覆盖每个方格一次。
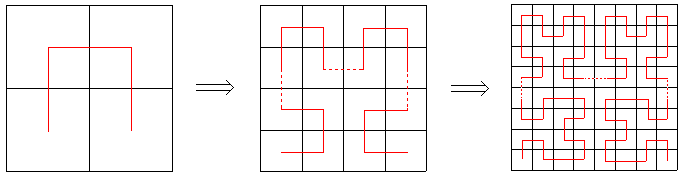
$H_n(n > 1)$可以通过如下方法构造:
1. 将 $H_n-1$ 顺时针旋转 90 度放在左下角;
2. 将 $H_n-1$ 逆时针旋转 90 度放在右下角;
3. 将 2 个 $H_n-1$ 分别放在左上角和右上角;
4. 用 3 条单位线段把 4 部分连接起来。
对于 $H_n$ 上每一个顶点 p ,我们定义 p 的坐标是它覆盖的小方格在矩阵中的坐标(左下角是(1, 1),右上角是$(2^n, 2^n)$,从左到右是 X 轴正方向,从下到上是 Y 轴正方向),定义 p 的序号是它在曲线上从起点开始数第几个顶点(从 1 开始计数)。
以下程序对于给定的 $n\ (n <= 30)$ 和 p 点坐标 $(x, y)$,输出 p 点的序号。
请仔细阅读分析源码,填写划线部分缺失的内容。
### 源代码
**C**
```c
#include
long long f(int n, int x, int y) {
if (n == 0) return 1;
int m = 1 << (n - 1);
if (x <= m && y <= m) {
return f(n - 1, y, x);
}
if (x > m && y <= m) {
return 3LL * m * m + f(n - 1, ________________ , m * 2 - x + 1); // 填空
}
if (x <= m && y > m) {
return 1LL * m * m + f(n - 1, x, y - m);
}
if (x > m && y > m) {
return 2LL * m * m + f(n - 1, x - m, y - m);
}
}
int main() {
int n, x, y;
scanf("%d %d %d", &n, &x, &y);
printf("%lld", f(n, x, y));
return 0;
}
```
**Java**
```java
import java.util.Scanner;
public class Main {
public static long f(int n, int x, int y) {
if (n == 0) return 1;
int m = 1 << (n - 1);
if (x <= m && y <= m) {
return f(n - 1, y, x);
}
if (x > m && y <= m) {
return 3L * m * m + f(n - 1, ________________ , m * 2 - x + 1); //填空
}
if (x <= m && y > m) {
return 1L * m * m + f(n - 1, x, y - m);
}
if (x > m && y > m) {
return 2L * m * m + f(n - 1, x - m, y - m);
}
return -1;
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int x = in.nextInt();
int y = in.nextInt();
System.out.println(f(n, x, y));
}
}
```