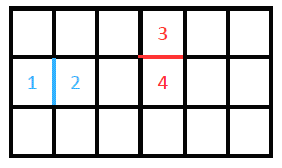
殖民地 ### 题目描述 带着殖民扩张的野心，Pear 和他的星际舰队登上 X 星球的某平原。为了评估这块土地的潜在价值，Pear 把它划分成了 $M \times N$ 格，每个格子上用一个整数（可正可负）表示它的价值。 Pear 要做的事很简单------选择一些格子，占领这些土地，通过建立围栏把它们和其它土地隔开。对于 $M \times N$ 的格子，一共有 $(M+1) \times N+M \times (N+1)$ 条围栏，即每个格子都有上下左右四个围栏；不在边界上的围栏被相邻的两个格子公用。大概如下图所示。  图中，蓝色的一段是围栏，属于格子 1 和 2 ；红色的一段是围栏，属于格子 3 和 4 。 每个格子有一个可正可负的收益，而建围栏的代价则一定是正的。 你需要选择一些格子，然后选择一些围栏把它们围起来，使得所有选择的格子和所有没被选的格子严格的被隔开。选择的格子可以不连通，也可以有"洞"，即一个连通块中间有一些格子没选。注意，若中间有"洞"，那么根据定义，"洞"和连通块也必须被隔开。 Pear 的目标很明确，花最小的代价，获得最大的收益。 ### 输入描述 输入第一行两个正整数 $M, N$，表示行数和列数。 接下来 $M$ 行，每行 $N$个整数，构成矩阵 $A$，$A_{i,j}$ 表示第 $i$$行第 $j\$ 列格子的价值。 接下来 $M+1$ 行，每行 $N$ 个整数，构成矩阵 $B$，$B_{i,j}$ 表示第 i 行第 j 列上方的围栏建立代价 特别的，$B_{M+1,j}$ 表示第 $M$ 行第 $j$ 列下方的围栏建立代价。 接下来 $M$ 行，每行 $N+1$ 个整数，构成矩阵 $C$，$C_{i,j}$ 表示第 $i$ 行第 $j$ 列左方的围栏建立代价，特别的，$C_{i,N+1}$ 表示第 $i$ 行第 $N$ 列右方的围栏建立代价。 其中，$M,N \leq 200$，$A、B、C$数组（所有的涉及到的格子、围栏输入数据）绝对值均不超过 1000。根据题意，$A$ 数组可正可负，$B、C$ 数组均为正整数。 ### 输出描述 输出一行。只有一个正整数，表示最大收益。 ### 输入输出样例 #### 示例 > 输入 ```txt 3 3 65 -6 -11 15 65 32 -8 5 66 4 1 6 7 3 11 23 21 22 5 25 22 26 1 1 13 16 3 3 4 6 3 1 2 ``` > 输出 ```txt 123 ```