编程题
割圆
### 题目描述
**本题为代码补全填空题,请将题目中给出的源代码补全,并复制到右侧代码框中,选择对应的编译语言(C/Java)后进行提交。若题目中给出的源代码语言不唯一,则只需选择其一进行补全提交即可。复制后需将源代码中填空部分的下划线删掉,填上你的答案。提交后若未能通过,除考虑填空部分出错外,还需注意是否因在复制后有改动非填空部分产生错误。**
南北朝时,我国数学家祖冲之首先把圆周率值计算到小数点后六位,比欧洲早了 1100 年!他采用的是称为“割圆法”的算法,实际上已经蕴含着现代微积分的思想。
如下图所示,圆的内接正六边形周长与圆的周长近似。多边形的边越多,接近的越好!我们从正六边形开始割圆吧。
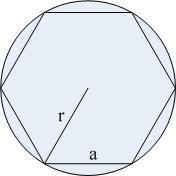
如下图所示,从圆心做弦的垂线,可把 6 边形分割为 12 边形。该 12 边形的边长 $a'$ 的计算方法很容易利用勾股定理给出。之后,再分割为正 24 边形,....如此循环会越来越接近圆周。
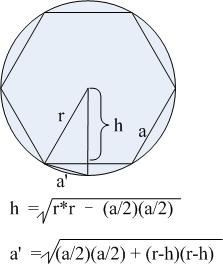
之所以从正六边开始,是因为此时边长与半径相等,便于计算。取半径值为 1,开始割圆吧!
以下代码描述了割圆过程。
程序先输出了标准圆周率值,紧接着输出了不断分割过程中多边形边数和所对应的圆周率逼近值。
请仔细阅读代码,并填写划线部分缺失的代码。
### 源代码
**Java**
```java
import java.util.*;
public class Main
{
public static void main(String[] args)
{
System.out.println("标准 " + Math.PI);
double a = 1;
int n = 6;
for(int i=0; i<10; i++)
{
double b = Math.sqrt(1-(a/2)*(a/2));
a = Math.sqrt((1-b)*(1-b) + (a/2)*(a/2));
n = ______________; //填空
System.out.println(n + " " + _______________); // 填空
}
}
}
```