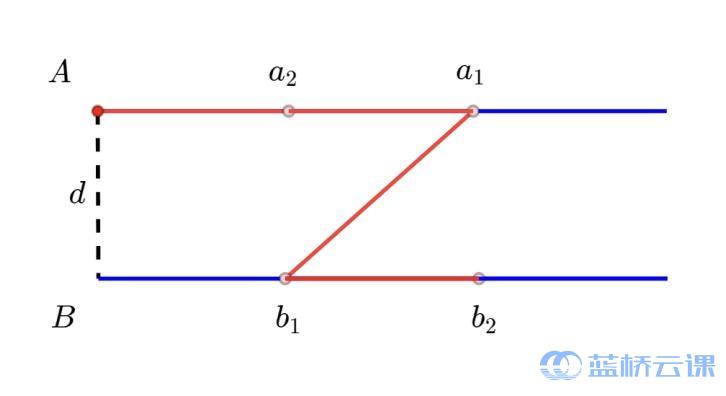
修路 ### 问题描述 这天, 小明在修路。 他需要修理两条平行的道路 $A, B$, 两条路上面分别有 $n$ 个和 $m$ 个点需要 维脩, 它们相对于道路起点的距离分别为 $a_{1}, a_{2}, \ldots, a_{n}$ 和 $b_{1}, b_{2}, b, \ldots, b_{m}=$ 如图, 两条路之间的距离为 $d$ 且它们起点 (最左端) 的连线和两条路都垂直。小明的起 点为道路 $A$ 的起点, 他需要尽可能快地逆历这些需要维修的 $n+m$ 个点, 他既 可以沿着道路 向右 行䞢, 也可以在两条道路之间的空地上**随意**行走。  小明想知道迻历这些点的最短路程是多少。 ### 输入格式 输入共三行，第一行为三个正整数 $n, m, d$ 。 第二行为 $n$ 个由空格㤱开的正整数 $a_{1}, a_{2}, \ldots, a_{n}$ 。 第三行为 $m$ 个由空格隔开的正整数 $b_{1}, b_{2}, \ldots, b_{m}$。 ### 输出格式 一行, 一个浮点数, 表示答案, 保留两位小数。 ### 样例输入 ```text 2 2 2 2 1 1 2 ``` ### 样例输出 ```text 5.24 ``` ### 样例说明 图中红线指出了样例的最短路线, $1+1+\sqrt{5}+1=5.24$ 。 ### 评测用例规模与约定 対于 $30 \\%$ 的数据, 保沚 $n+m \leq 10$; 对于 $100 \\%$ 的数据, 保证 $n, m \leq 2000, d \leq 4 \times 10^{6}, a_{i}, b_{i} \leq 10^{6}$ 。