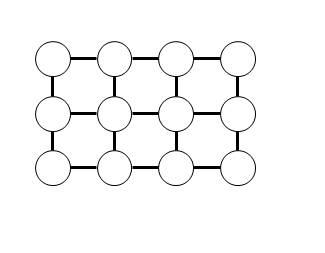
生成树计数 ### 题目描述 给定一个 $n\times m$ 的格点图，包含 $n$ 行 $m$ 列共 $n \times m$ 个顶点，相邻的顶点之间有一条边。 下图给出了一个 $3 \times 4$ 的格点图的例子。  如果在图中删除部分顶点和其相邻的边，如上图删除第 2 行第 3 列和第 3 行第 1 列的顶点后，如下图所示。  图的生成树指包含图中的所有顶点和其中的一部分边，使得任意两个顶点之间都有由边构成的唯一路径。如果两个生成树包含有不同的边即被认为不同，则上图中共有 31 种不同的生成树，其中 $a$ 边不选有 10 种，$a$ 边选有 21 种。 给出格点图中保留的顶点的信息，请计算该图一共有多少种不同的生成树。 ### 输入描述 输入的第一行包含两个整数 $n, m$，用空格分隔，表示格点图的行数和列数。 接下来 $n$ 行，每行 $m$ 个字母（中间没有分隔字符），每个字母必然是大写 $E$ 或大写 $N$，$E$ 表示对应的顶点存在，$N$ 表示对应的顶点不存在。保证存在至少一个顶点。 其中，$1 \leq n \leq 6$，$1 \leq m \leq 10^5$。 例如： 样例输入： 3 4 EEEE EENE NEEE ### 输出描述 输出一行，包含一个整数，表示生成树的个数。答案可能很大，你只需要计算答案除以 $10^9+7$ 的余数即可。 ### 输入输出样例 #### 示例 > 输入 ```txt 3 4 EEEE EENE NEEE ``` > 输出 ```txt 31 ```