1719：过河

【题目描述】

EE想搭一座跨过河的桥。河是一条无限长的宽度为$W$的直线，所有在直角坐标系中符合$0≤y≤W$的点都属于这条河流。

河面上有$N$个木桩，还有$M$种可以用的木头圆盘，第$k$个木桩的坐标为($X_k,Y_k$)。第 $k$ 种圆盘半径为$R_k$,每一块的价格为$C_k$。

EE可以买任意多的圆盘，而且他可以把它们放到河面上。每一个圆盘的中心都必须为某一个木桩的位置。注意，某些圆盘的一部分可以在地面上($y < 0,W < y$).

EE只能在直线$y=0$或直线$y=W$或圆盘上移动（相切的两者之间可以移动）。请问从直线$y=0$到直线$y=$修建一座可以走过去的桥最少的花费。

【输入】

第一行一个整数$T$，代表测试数据的数量。

接下来 $T$ 组数据。每组数据的第一行有三个空格隔开的整数 $N,M,W$。

接下来 $N$ 行，每行$2$个空格隔开的整数 $X_k,Y_k$。

接下来 $M$ 行，每行$2$个空格隔开的整数 $R_k,C_k$。

【输出】

对于每组数据，输出从直线$y=0$到直线$y=W$修建一座可以走过去的桥最少的花费，假如这是不可能的，那么输出“$impossible$”（不带引号）。

【输入样例】

3
11 4 13
19 10
8 7
11 4
26 1
4 2
15 4
19 4
1 9
4 6
19 5
15 10
2 1
3 100
4 10000
5 1000000
11 4 13
19 10
8 7
11 4
26 1
4 2
15 4
19 4
1 9
4 6
19 5
15 10
2 1
3 2
4 3
5 4
1 1 1000000000
0 500000000
1 1

【输出样例】

206
5
impossible

【提示】

【样例解释】

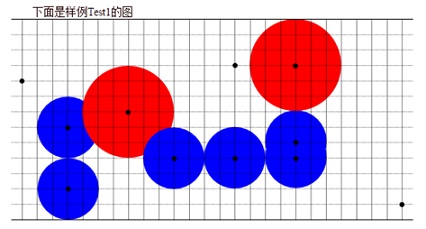
【数据规模】

对于10%的数据，$N,M≤5$；

对于30%的数据，$N,M≤30$；

另有20%的数据，$X_k = 0$；

对于70%的数据，$N,M≤100$；

对于100%的数据，$1≤T≤10；1≤N,M≤250； 2≤W≤10^9$；

$0≤X_k≤10^9；1≤Y_k≤W；1≤R_k≤10^9；1≤C_k≤10^6$。