编程实现：

蚂蚁王国住着 N 只蚂蚁，每只蚂蚁都有自己的领地，领地之间可以直接到达或经过其他领地间接到达，可以直接到达的领地之间的道路距离都为 1，但所有领地都有一条唯一的最短路径可以相互到达。

现要在 N 块领地（依次编号为 1~N）中，选出一块领地建立游乐场，使得所有蚂蚁到游乐场的最小距离总和是 N 种情况中最小的。

例如：N = 8，1~8 号领地之间的连接关系为：1 和 5、2 和 6、3 和 6、4 和 5、5 和 6、4 和 7、5 和 8。

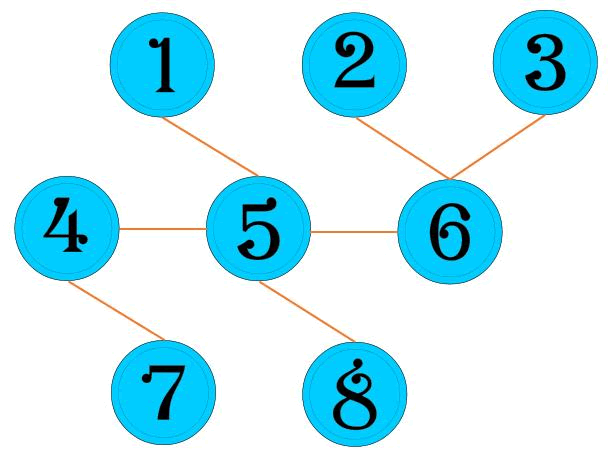
如果将游乐场创建在 5 号领地，最小距离总和为 10。

1 号到 5 号距离为 1；2 号到 5 号距离为 2；3 号到 5 号距离为 2；4 号到 5 号距离为 1；6 号到 5 号距离为 1；

7 号到 5 号距离为 2；8 号到 5 号距离为 1。

如果将游乐场创建在 6 号领地，最小距离总和为 12。

1 号到 6 号距离为 2；2 号到 6 号距离为 1；3 号到 6 号距离为 1；4 号到 6 号距离为 2；5 号到 6 号距离为 1；

7 号到 6 号距离为 3；8 号到 6 号距离为 2。

……

可以发现，将游乐场创建在 5 号领地，最小距离总和 10 是最小的，故输出 10。

输入描述：

第一行输入一个正整数 N（2≤N≤20），表示领地数量

接下来输入 N-1 行，每行包含两个正整数（1≤正整数≤N，两个正整数不相同），表示两块领地相互之间可以直接到达，正整数之间以一个英文逗号隔开（数据保证 N 块领地相互之间可以到达）

输出描述：

输出一个整数，表示 N 种情况中最小距离总和的最小值

样例输入：

8
1,5
2,6
3,6
4,5
5,6
4,7
5,8

样例输出：

10