纪念品

【问题描述】

小伟突然获得一种超能力，他知道未来T天N种纪念品每天的价格。某个纪念品  的价格是指购买一个该纪念品所需的金币数量，以及卖出一个该纪念品换回的金币数量。

每天，小伟可以进行以下两种交易无限次：

1. 任选一个纪念品，若手上有足够金币，以当日价格购买该纪念品；

2. 卖出持有的任意一个纪念品，以当日价格换回金币。

每天卖出纪念品换回的金币可以立即用于购买纪念品，当日购买的纪念品也可以当 日卖出换回金币。当然， 一直持有纪念品也是可以的。

T天之后，小伟的超能力消失。因此他一定会在第T天卖出所有纪念品换回金币。 小伟现在有M枚金币，他想要在超能力消失后拥有尽可能多的金币。

【输入格式】

输入文件名为souvenir . in。

第一行包含三个正整数T,N,M,相邻两数之间以一个空格分开，分别代表未来天数 T,纪念品数量N,小伟现在拥有的金币数量M。

接下来T行，每行包含N个正整数，相邻两数之间以一个空格分隔。第i行的N个正整数分别为Pi1,Pi2, …… ,Pin,其中Pi,j表示第i天第j种纪念品的价格。

【输出格式】

输出文件名为souvenir . out。

输出仅一行，包含一个正整数，表示小伟在超能力消失后最多能拥有的金币数量。

【输入输出样例1】

【 输入输出样例1说明】

最佳策略是：

第二天花光所有100枚金币买入5个纪念品1;

第三天卖出5个纪念品1,获得金币125枚；

第四天买入6个纪念品1,剩余5枚金币；

第六天必须卖出所有纪念品换回300枚金币，第四天剩余5枚金币，共305枚金币。

超能力消失后，小伟最多拥有305枚金币。

【输入输出样例2】

【输入输出样例2说明】

最佳策略是：

第一天花光所有金币买入10个纪念品1;

第二天卖出全部纪念品1得到150枚金币并买入8个纪念品2和1个纪念品3,剩 余1枚金币；

第三天必须卖出所有纪念品换回216枚金币，第二天剩余1枚金币，共217枚金币。 超能力消失后，小伟最多拥有217枚金币。

【数据规模与约定】

对于10%的数据，T=1。

对于30%的数据，T≤4,N≤4,M≤100,所有价格10≤Pij≤100。 

另有15%的数据，T≤100,N=1。

另有15%的数据，T=2,N≤100。

对于100%的数据，T≤100,N≤100,M≤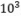,所有价格1≤Pij≤10⁴,数 据保证任意时刻，小明手上的金币数不可能超过10⁴。