1450：【例 3】Knight Moves

【题目描述】

原题来自：POJ 1915

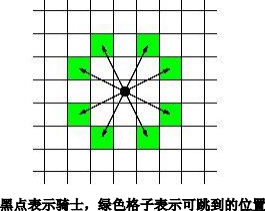
编写一个程序，计算一个骑士从棋盘上的一个格子到另一个格子所需的最小步数。骑士一步可以移动到的位置由下图给出。

【输入】

第一行给出骑士的数量 $n$。

在接下来的 $3n$ 行中，每 $3$ 行描述了一个骑士。其中，

第一行一个整数 $L$ 表示棋盘的大小，整个棋盘大小为 $L×L$；

第二行和第三行分别包含一对整数 ($x,y$)，表示骑士的起始点和终点。假设对于每一个骑士，起始点和终点均合理。

【输出】

对每一个骑士，输出一行一个整数表示需要移动的最小步数。如果起始点和终点相同，则输出 $0$。

【输入样例】

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1

【输出样例】

5
28
0

【提示】

对于 100% 的数据，有 $4≤L≤300$，保证 $0≤x,y≤L−1$。