烹饪问题
时间限制:1.0 s
内存限制:128.0 MB
问题描述
有N种食材,编号从0至N-1,其中第i种食材的美味度为ai。
不同食材之间的组合可能产生奇妙的化学反应。具体来说,如果两种食材的美味度分别为x和y,那么它们的契合度为x and y。
其中,and运算为按位与运算,需要先将两个运算数转换为二进制,然后在高位补足0,再逐位进行与运算。例如,12与6的二进制表示分别为 1100 和 0110 ,将它们逐位进行与运算,得到 0100 ,转换为十进制得到4,因此12 and 6=4。在 C++ 或 Python 中,可以直接使用 & 运算符表示与运算。
现在,请你找到契合度最高的两种食材,并输出它们的契合度。
输入描述
第一行一个整数N,表示食材的种数。
接下来一行N个用空格隔开的整数,依次为a0,…,aN-1,表示各种食材的美味度。
输出描述
输出一行一个整数,表示最高的契合度。
特别提醒
在常规程序中,输入、输出时提供提示是好习惯。但在本场考试中,由于系统限定,请不要在输入、输出中附带任何提示信息。
样例输入 1
3
1 2 3
样例输出 1
2
样例解释 1
可以编号为1,2的食材之间的契合度为2 and 3=2,是所有食材两两之间最高的契合度。
样例输入 2
5
5 6 2 10 13
样例输出 2
8
样例解释 1
可以编号为3,4的食材之间的契合度为10 and 13=8,是所有食材两两之间最高的契合度。
数据规模
对于40%的测试点,保证N≤1000;
对于所有测试点,保证N≤106,0≤ai≤2147483647。
小杨的幸运数
时间限制:5.0 s
内存限制:128.0 MB
问题描述
小杨认为,所有大于等于a的完全平方数都是他的超级幸运数。
小杨还认为,所有超级幸运数的倍数都是他的幸运数。自然地,小杨的所有超级幸运数也都是幸运数。
对于一个非幸运数,小杨规定,可以将它一直+1,直到它变成一个幸运数。我们把这个过程叫做幸运化。例如,如果a=4,那么4是最小的幸运数,而1不是,但我们可以连续对1做3次+1操作,使其变为4,所以我们可以说,1幸运化后的结果是4。
现在,小样给出N个数,请你首先判断它们是不是幸运数;接着,对于非幸运数,请你将它们幸运化。
输入描述
第一行 2 个正整数a,N。
接下来N行,每行一个正整数x,表示需要判断(幸运化)的数。
输出描述
输出N行,对于每个给定的x,如果它是幸运数,请输出lucky ,否则请输出将其幸运化后的结果。
特别提醒
在常规程序中,输入、输出时提供提示是好习惯。但在本场考试中,由于系统限定,请不要在输入、输出中附带任何提示信息。
样例输入 1
2 4
1
4
5
9
样例输出 1
4
lucky
8
lucky
样例解释 1
1虽然是完全平方数,但它小于a,因此它并不是超级幸运数,也不是幸运数。将其进行3次+1操作后,最终得到幸运数4。
4是幸运数,因此直接输出 lucky 。
5不是幸运数,将其进行3次+1操作后,最终得到幸运数8。
9是幸运数,因此直接输出 lucky 。
样例输入 2
16 11
1
2
4
8
16
32
64
128
256
512
1024
样例输出 2
16
16
16
16
lucky
lucky
lucky
lucky
lucky
lucky
lucky
数据规模
对于30%的测试点,保证a,x≤100,N≤100 。
对于60%的测试点,保证a,x≤106。
对于所有测试点,保证a≤1000001;保证N≤2×105;保证1≤x≤1000001。
下面Python代码用于有序 list 的二分查找,有关说法错误的是( )。
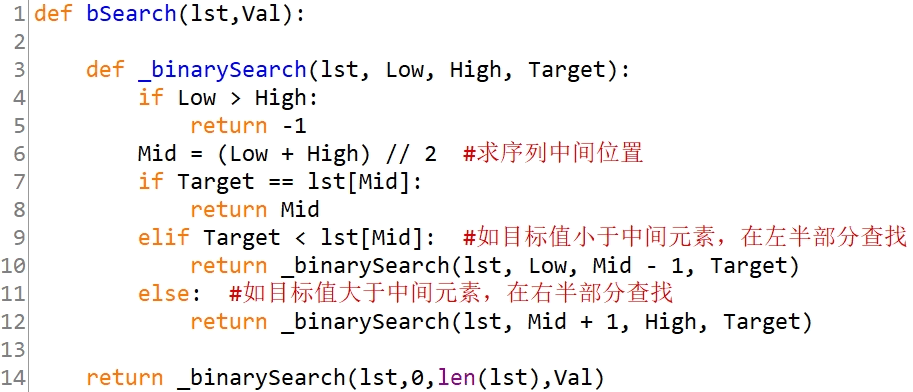
代码采用二分法实现有序list的查找
代码采用分治算法实现有序list的查找
代码采用递归方式实现有序list的查找
代码采用动态规划算法实现有序list的查找
有关下面Python代码的说法正确的是( )。

上述代码构成单向链表
上述代码构成双向链表
上述代码构成循环链表
上述代码构成指针链表
下面的Python用于对 lstA 排序,使得偶数在前奇数在后,横线处不应填入( )。

key = not isEven
key = lambda x: isEven(x), reverse = True
key = isEven, reverse = True
key = lambda x: not isEven(x)
阅读下面的Python代码,执行后其输出是( )。

1->120<===>2->120
1->120<===>1->120
1->120<===>1->2->3->4->5->120
1->120<===>2->3->4->5->6->120
有关下面Python代码正确的是( )。

True True False
False True False
False False True
触发异常
下面的Python代码实现对 list 的快速排序,有关说法,错误的是( )。
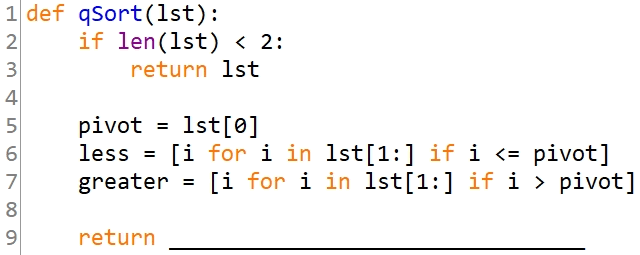
qSort(less) + qSort(greater) + [pivot]
[pivot] + qSort(less) + qSort(greater)
qSort(less) + [pivot] + qSort(greater)
qSort(less) + pivot + qSort(greater)
下面Python代码以递归方式实现合并排序,并假设 merge(left,right) 函数能对有序(同样排序规则)的left 和 right 排序。横线处应填上代码是( )。

mergeSort(listData[:Middle]), mergeSort(listData[Middle:])
mergeSort(listData[:Middle-1]), mergeSort(listData[Middle+1:])
mergeSort(listData[:Middle]), mergeSort(listData[Middle+1:])
mergeSort(listData[:Middle-1]), mergeSort(listData[Middle:])
下面的Python代码用于实现每个字符后紧跟随字符及其出现次数,并对紧跟随字符排序,即出现次数最多排在前,形如: {'中': [('文', 1), ('国', 2), ('华', 2)]} ,此处 S 仅是部分字符,可能很多,横线处应填入代码是( )。

x[0]:x[1].items().sort(key = lambda x:x[1], reverse = True)
x[0]:x[1].items().sort(key = lambda x:x[0], reverse = True)
x[0]:sorted(x[1].items(), key = lambda x:-x[0])
x[0]:sorted(x[1].items(), key = lambda x:-x[1])
下面Python代码用于求斐波那契数列,该数列第1、2项为1,以后各项均是前两项之和。下面有关说法错误的是( )。

fiboA( ) 用递归方式, fiboB() 循环方式
fiboA( ) 更加符合斐波那契数列的数学定义,直观易于理解,而 fiboB() 需要将数学定义转换为计算机程序实现
fiboA( ) 不仅仅更加符合数学定义,直观易于理解,且因代码量较少执行效率更高
fiboB( ) 虽然代码量有所增加,但其执行效率更高
下面的Python代码用于排序 sA 字符串中每个字符出现的次数(字频), sA 字符串可能很长,此处仅为示例。排序要求是按字频降序,如果字频相同则按字符的ASCII升序,横线处应填入代码是( )。

charCount, key = lambda x:(-x[1],x[0])
charCount.items(), key = lambda x:(-x[1],ord(x[0]))
charCount.items(), key = lambda x:(x[1],-ord(x[0]))
触发异常,不能对字典进行排序。
内排序有不同的类别,下面哪种排序算法和冒泡排序是同一类?( )
希尔排序
快速排序
堆排序
插入排序
下面Python代码中的 isPrimeA() 和 isPrimeB() 都用于判断参数N是否素数,有关其时间复杂度的正确说法是( )。

isPrimeA( ) 的最坏时间复杂度是 , isPrimeB( ) 的最坏时间复杂度是 ,isPrimeA()优于isPrimeB()
isPrimeA() 的最坏时间复杂度是 , isPrimeB( ) 的最坏时间复杂度是 ,isPrimeB()绝大多数情况下优于isPrimeA()
isPrimeA() 的最坏时间复杂度是 , isPrimeB( ) 的最坏时间复杂度是 , isPrimeA( ) 优于isPrimeB( )
isPrimeA() 的最坏时间复杂度是 , isPrimeB( ) 的最坏时间复杂度是 ,isPrimeA()优于isPrimeB( )
通讯卫星在通信网络系统中主要起到( )的作用。
信息过滤
信号中继
避免攻击
数据加密
小杨想编写一个判断任意输入的整数N是否为素数的程序,下面哪个方法不合适?( )
埃氏筛法
线性筛法
二分答案
枚举法
在上题的算法中,其时间复杂度是( )。
O(N)
O(logN)
O(NlogN)
O(N2)
贪心算法可以达到局部最优,但可能不是全局最优解。 ( )
正确
错误
以下Python代码能以递归方式实现斐波那契数列,该数列第1、2项为1,以后各项均是前两项之和。( )

正确
错误
在Python中,当对 list 类型进行 in 运算查找元素是否存在时,其查找通常采用二分法。( )
正确
错误
插入排序有时比快速排序时间复杂度更低。( )
正确
错误
如果自定已class已经定义了 __lt__() 魔术方法,则自动支持内置函数 sorted() 。( )
正确
错误
小杨想写一个程序来算出正整数N有多少个因数,经过思考他写出了一个重复没有超过N/2次的循环就能够算出来了。( )
正确
错误
下面的Python代码能实现十进制正整数N转换为八进制并输出。( )

正确
错误
归并排序的时间复杂度是 。( )
正确
错误
Python代码 print(sorted(list(range(10)), key = lambda x:x % 5)) 执行后将输出 [0, 5, 1,6, 2, 7, 3, 8, 4, 9] 。( )
正确
错误
同样的整数序列分别保存在单链表和双向链中,这两种链表上的简单冒泡排序的复杂度相同。( )
正确
错误