下面C++代码用于求斐波那契数列,该数列第1、2项为1,以后各项均是前两项之和。函数fibo()属于( )。

枚举算法
贪心算法
迭代算法
递归算法
下面C++代码用于将输入金额换成最少币种组合方案,其实现算法是( )。
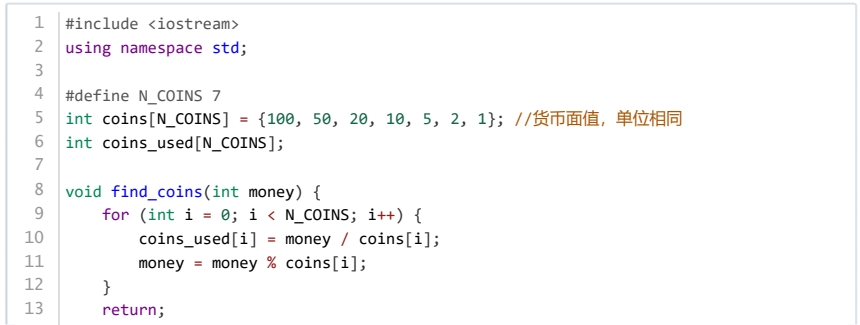
枚举算法
贪心算法
迭代算法
递归算法
小杨采用如下双链表结构保存他喜欢的歌曲列表:

小杨想在头指针为 head 的双链表中查找他喜欢的某首歌曲,采用如下查询函数,该操作的时间复杂度为( )。

小杨想在如上题所述的双向链表中加入一首新歌曲。为了能快速找到该歌曲,他将其作为链表的第一首歌曲,则下面横线上应填入的代码为( )。

head->next->prev = p;
head->next = p;
head->prev = p;
触发异常,不能对空指针进行操作。
下面是根据欧几里得算法编写的函数,它计算的是 a与 b的( )。

最小公倍数
最大公共质因子
最大公约数
最小公共质因子
欧几里得算法还可以写成如下形式:

下面有关说法,错误的是( )。
本题的 gcd() 实现为递归方式。
本题的 gcd() 代码量少,更容易理解其辗转相除的思想。
当 a较大时,本题的 gcd() 实现会多次调用自身,需要较多额外的辅助空间。
当 a较大时,相比上题中的 gcd() 的实现,本题的 gcd() 执行效率更高。
下述代码实现素数表的线性筛法,筛选出所有小于等于n 的素数,则横线上应填的代码是( )。
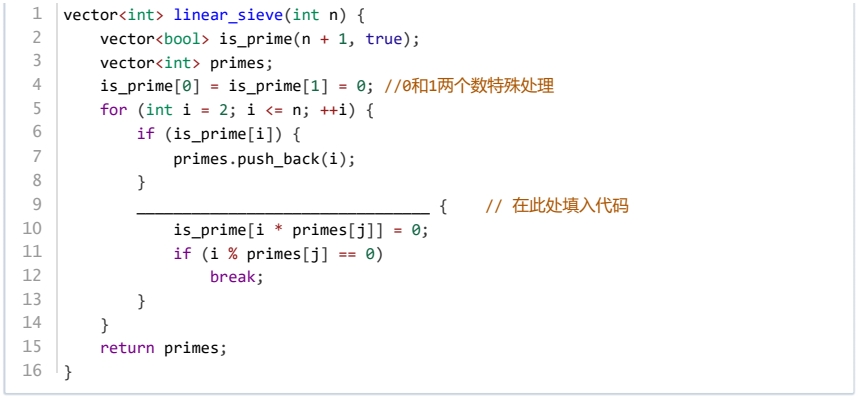
for (int j = 0; j < primes.size() && i * primes[j] <= n; j++)
for (int j = 0; j <= sqrt(n) && i * primes[j] <= n; j++)
for (int j = 0; j <= n; j++)
for (int j = 1; j <= sqrt(n); j++)
上题代码的时间复杂度是( )。
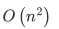
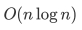
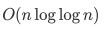
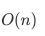
为了正确实现快速排序,下面横线上的代码应为( )。

while (i <= mid)
while (i < mid)
while (i < j)
while (i <= j)
关于分治算法,以下哪个说法正确?
分治算法将问题分成子问题,然后分别解决子问题,最后合并结果。
归并排序不是分治算法的应用。
分治算法通常用于解决小规模问题。
分治算法的时间复杂度总是优于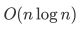
根据下述二分查找法,在排好序的数组 1,3,6,9,17,31,39,52,61,79,81,90,96 中查找数值82,和82比较的数组元素分别是( )。

52, 61, 81, 90
52, 79, 90, 81
39, 79, 90, 81
39, 79, 90
要实现一个高精度减法函数,则下面代码中加划线应该填写的代码为( )。

a[i + 1]--;
a[i]--;
b[i + 1]--;
b[i]--;
设A 和 B是两个长度为m 的有序数组,现将A 和 B合并成一个有序数组,归并排序算法在最坏情况下至少要做( )次比较。
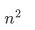
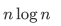
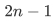
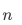
给定如下函数:

则当n=7时,函数返回值为( )。
0
1
21
-11
给定如下函数(函数功能同上题,增加输出打印):

则当 n=4时,屏幕上输出序列为( )。
4 3 2 1
1 2 3 4
4 2 3 1 2
4 2 3 2 1
如果将双向链表的最后一个结点的下一项指针指向第一个结点,第一个结点的前一项指针指向最后一个结点,则该双向链表构成循环链表。
对
错
数组和链表都是线性表,链表的优点是插入删除不需要移动元素,并且能随机查找。
对
错
链表的存储空间物理上可以连续,也可以不连续。
对
错
找出自然数n以内的所有质数,常用算法有埃拉托斯特尼(埃氏)筛法和线性筛法,其中埃氏筛法效率更高。
对
错
唯一分解定理表明任何一个大于1的整数都可以唯一地表示为一系列质数的乘积,即质因数分解是唯一的。
对
错
贪心算法通过每一步选择局部最优解来获得全局最优解,但并不一定能找到最优解。
对
错
归并排序和快速排序都采用递归实现,也都是不稳定排序。( )
对
错
插入排序有时比快速排序时间复杂度更低。
对
错
在进行全国人口普查时,将其分解为对每个省市县乡来进行普查和统计。这是典型的分治策略。
对
错
在下面C++代码中,由于删除了变量 ptr ,因此 ptr 所对应的数据也随之删除,故执行下述代码时,将报错。

对
错
黑白格
题面描述
小杨有一个 n行 m列的网格图,其中每个格子要么是白色,要么是黑色。
小杨想知道至少包含 k个黑色格子的最小子矩形包含了多少个格子。
输入格式
第一行包含三个正整数n,m,k ,含义如题面所示。
之后n 行,每行一个长度为m 的 01串,代表网格图第 i行格子的颜色,如果为 0,则对应格子为白色,否则为黑色
输出格式
输出一个整数,代表至少包含k 个黑色格子的最小子矩形包含格子的数量,如果不存在则输出 0。
样例1
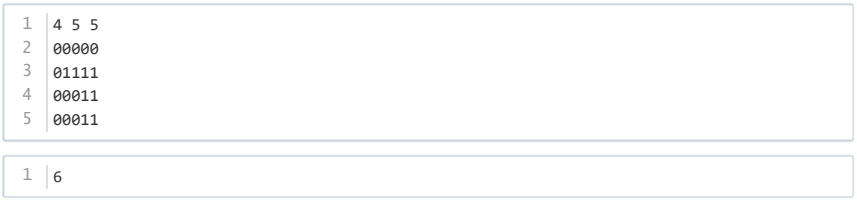
样例解释
对于样例1,假设 (i,j ) 代表第 i行第 j列,至少包含 5个黑色格子的最小子矩形的四个顶点为 ( 2,4),( 2,5),( 4,4),(4,5),共包含 6个格子。
数据范围

小杨的幸运数字
题面描述
小杨认为他的幸运数字应该恰好有两种不同的质因子,例如,12=2×2 ×3的质因子有 2,3,恰好为两种不同的质因子,因此12 是幸运数字,而30=2×3×5 的质因子有 2,3,5,不符合要求,不为幸运数字。
小杨现在有 n个正整数,他想知道每个正整数是否是他的幸运数字。
输入格式
第一行包含一个正整数n ,代表正整数个数。
之后n 行,每行一个正整数。
输出格式
输出n 行,对于每个正整数,如果是幸运数字,输出 1,否则输出 0。
样例1
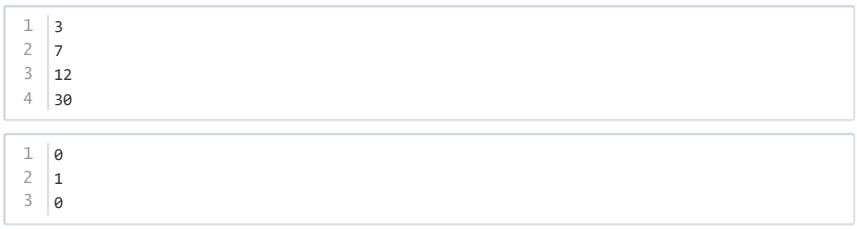
样例解释
7的质因子有7,只有1种。
12的质因子有2,3,恰好有两种。
30的质因子有2,3,5,三种。
数据范围
